Section 1.2 — Data in practice

This notebook contains all the code from Section 1.2 Data in practice of the No Bullshit Guide to Statistics.

Getting started with JupyterLab

Download and install JupyterLab Desktop

Follow instructions in the Python tutorial to install JupyterLab Desktop on your computer.

Download the noBSstats notebooks and datasets

Go to URL minireference/noBSstats and use the Code dropdown button to download the ZIP archive of the entire repository.

After downloading the ZIP archive, double-click on the file to extract its contents, and move the resulting folder noBSstats to a location on your computer where you normally keep your documents.

The ZIP archive includes all the datasets and computational notebooks for the book. Use the File browser pane on the right to navigate to the location where you saved the noBSstats folder and explore the subfolders datasets, notebooks, exercises, tutorials, etc.

Datasets for the book

The datasets folder contains all the datasets used in examples and exercises throughout the book.

id	filename	relative path	url
0	players.csv	../datasets/players.csv	https://noBSstats.com/datasets/players.csv
1	apples.csv	../datasets/apples.csv	https://noBSstats.com/datasets/apples.csv
2	eprices.csv	../datasets/eprices.csv	https://noBSstats.com/datasets/eprices.csv
2w	epriceswide.csv	../datasets/epriceswide.csv	https://noBSstats.com/datasets/epriceswide.csv
3	students.csv	../datasets/students.csv	https://noBSstats.com/datasets/students.csv
4	kombucha.csv	../datasets/kombucha.csv	https://noBSstats.com/datasets/kombucha.csv
4p	kombuchapop.csv	../datasets/kombuchapop.csv	https://noBSstats.com/datasets/kombuchapop.csv
5	doctors.csv	../datasets/doctors.csv	https://noBSstats.com/datasets/doctors.csv
6	visitors.csv	../datasets/visitors.csv	https://noBSstats.com/datasets/visitors.csv
D	minimal.csv	../datasets/minimal.csv	https://noBSstats.com/datasets/minimal.csv

Interactive notebooks for each section

The notebooks folder contains the jupyter notebooks associated with each section of the book, similar to the one you’re currently looking at.

section	notebook name
Section 1.1	11_intro_to_data.ipynb
Section 1.2	12_data_in_practice.ipynb
Section 1.3	13_descriptive_statistics.ipynb
Section 2.1	21_discrete_random_vars.ipynb
Section 2.2	22_multiple_random_vars.ipynb
Section 2.3	23_inventory_discrete_dists.ipynb
Section 2.4	24_calculus_prerequisites.ipynb
Section 2.5	25_continuous_random_vars.ipynb
Section 2.6	26_inventory_continuous_dists.ipynb
Section 2.7	27_random_var_generation.ipynb
Section 2.8	28_random_samples.ipynb
Section 3.1	31_estimators.ipynb
Section 3.2	32_confidence_intervals.ipynb
Section 3.3	33_intro_to_NHST.ipynb
Section 3.4	34_analytical_approx.ipynb
Section 3.5	35_two_sample_tests.ipynb
Section 3.6	36_design.ipynb
Section 3.7	37_inventory_stats_tests.ipynb
Section 4.1	41_introduction_to_LMs.ipynb

Exercises notebooks

The exercises folder contains starter notebooks for the exercises in each section.

section	notebook name
Section 1.2	exercises_12_practical_data.ipynb
Section 1.3	exercises_13_descr_stats.ipynb
Section 2.1	exercises_21_discrete_RVs.ipynb
Section 3.1	exercises_31_estimtors.ipynb
Section 3.2	exercises_32_confidence_intervals.ipynb
Section 3.3	exercises_33_intro_to_NHST.ipynb
Section 3.5	exercises_35_two_sample_tests.ipynb

Data management with Pandas

The first step is to import the Pandas library. We’ll follow the standard convention of importing the pandas module under the alias pd.

import pandas as pd

Loading datasets

Players dataset

Consider the data file players.csv is located in the datasets directory. The file extension .csv tells us the file contains text data formatted as Comma-Separated Values (CSV). We can use the command %pycat to print the raw contents of the this file.

%pycat ../datasets/players.csv

We see the file contains 13 lines of text, and each line contains—as promised by the .csv file extension—values separated by commas. The first line in the data file is called the “header” and contains the names of the variable names.

We can create a the data frame object from the players dataset located at ../datasets/players.csv by calling the function pd.read_csv.

players = pd.read_csv("../datasets/players.csv")
players

	username	country	age	ezlvl	time	points	finished
0	mary	us	38	0	124.94	418	0
1	jane	ca	21	0	331.64	1149	1
2	emil	fr	52	1	324.61	1321	1
3	ivan	ca	50	1	39.51	226	0
4	hasan	tr	26	1	253.19	815	0
5	jordan	us	45	0	28.49	206	0
6	sanjay	ca	27	1	350.00	1401	1
7	lena	uk	23	0	408.76	1745	1
8	shuo	cn	24	1	194.77	1043	0
9	r0byn	us	59	0	255.55	1102	0
10	anna	pl	18	0	303.66	1209	1
11	joro	bg	22	1	381.97	1491	1

Data frame properties

What type of object is players ?

type(players)

pandas.core.frame.DataFrame

The players data frame object has a bunch of useful properties (attributes) and functions (methods) “attached” to it, which we can access using the dot syntax.

The shape of the players data frame

players.shape

(12, 7)

The rows index

len(players.index)

12

players.index

RangeIndex(start=0, stop=12, step=1)

list(players.index)

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]

The columns index

len(players.columns)

7

players.columns

Index(['username', 'country', 'age', 'ezlvl', 'time', 'points', 'finished'], dtype='object')

list(players.columns)

['username', 'country', 'age', 'ezlvl', 'time', 'points', 'finished']

Exploring data frame objects

players.head(3)
# players.tail(3)
# players.sample(3)

	username	country	age	ezlvl	time	points	finished
0	mary	us	38	0	124.94	418	0
1	jane	ca	21	0	331.64	1149	1
2	emil	fr	52	1	324.61	1321	1

Data types

players.dtypes

username     object
country      object
age           int64
ezlvl         int64
time        float64
points        int64
finished      int64
dtype: object

players.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 12 entries, 0 to 11
Data columns (total 7 columns):
 #   Column    Non-Null Count  Dtype  
---  ------    --------------  -----  
 0   username  12 non-null     object 
 1   country   12 non-null     object 
 2   age       12 non-null     int64  
 3   ezlvl     12 non-null     int64  
 4   time      12 non-null     float64
 5   points    12 non-null     int64  
 6   finished  12 non-null     int64  
dtypes: float64(1), int64(4), object(2)
memory usage: 800.0+ bytes

Accessing values in a DataFrame

Selecting individual values

The player with username emil has index 2 in the data frame. To see the value of the points variable for the player emil, we use the following expression based on the .loc[] selector syntax.

players.loc[2,"points"]

1321

Selecting entire rows

Let’s now select all the measurements we have for Sanjay (the player at index 6).

players.loc[6,:]  # == players.loc[6]

username    sanjay
country         ca
age             27
ezlvl            1
time         350.0
points        1401
finished         1
Name: 6, dtype: object

Selecting entire columns

We use the square brackets to select columns from a data frame. For example, this is how we extract the "age" column from the players data frame.

players["age"]

0     38
1     21
2     52
3     50
4     26
5     45
6     27
7     23
8     24
9     59
10    18
11    22
Name: age, dtype: int64

Selecting multiple columns

We can select multiple columns by using list of column names inside the square brackets.

players[ ["username","country"] ]

	username	country
0	mary	us
1	jane	ca
2	emil	fr
3	ivan	ca
4	hasan	tr
5	jordan	us
6	sanjay	ca
7	lena	uk
8	shuo	cn
9	r0byn	us
10	anna	pl
11	joro	bg

Statistical calculations using Pandas

Let’s extract the values from the "age" column from the players data frame and store them as new variable called ages. We intentionally choose the name ages (plural of the column name) to remember where the data comes from.

ages = players["age"]
ages

0     38
1     21
2     52
3     50
4     26
5     45
6     27
7     23
8     24
9     59
10    18
11    22
Name: age, dtype: int64

The variable ages is a Pandas series object.

type(ages)

pandas.core.series.Series

We can access individual values within the series ages using the square brackets.

ages[6]

27

Series attributes

The Pandas series ages has the same index as the players data frame.

ages.index

RangeIndex(start=0, stop=12, step=1)

The series ages also “remembers” the name of the column from which it was extracted.

ages.name

'age'

We sometimes want to see the data without the index. We can do this by accessing the .values attribute of the series.

ages.values

array([38, 21, 52, 50, 26, 45, 27, 23, 24, 59, 18, 22])

Series methods

ages.count()

12

Alternatively, since series objects are list-like, we can use the Python build in function len to find the length of the series.

len(ages)

12

ages.sum()

405

The average value of a list of \(n\) values \(\mathbf{x} = [x_1, x_2, \ldots, x_n]\) is computed using the formula \(\overline{\mathbf{x}} = \tfrac{1}{n}\!\left( x_1 + x_2 + \cdots + x_n \right)\). This formula says that the average is computed by summing together all the values in the list \(\mathbf{x}\) and dividing by the length of the list \(n\).

The expression for computing the average age using Pandas methods is as follows:

ages.sum() / ages.count()

33.75

An equivalent, more direct, way to compute the arithmetic mean of the values in the series ages is to call its .mean() method.

ages.mean()

33.75

The standard deviation (dispersion from the mean) is another common statistic that we might want to calculate for a variable in a dataset.

ages.std()

14.28365244861157

Pandas series and data frames objects have numerous other methods for computing numerical data summaries, which are called the descriptive statistics of the variable. We’ll learn more about those in Section 1.3 Descriptive statistics.

Selecting only certain rows (filtering)

We often want to select a subset of the rows of a data frame that fit one or more criteria. This is equivalent to “filtering out” the rows that don’t satisfy these criteria. We use a two-step procedure for this:

• Step 1: Build a “selection mask” series that consists of boolean values (True or False).

• Step 2: Select the subset of rows from the data frame using the mask. The result is a new data frame that contains only the rows that correspond to the True values in the selection mask.

To select only rows where ezlvl is 1, we first build the boolean selection mask (Step 1)…

mask = players["ezlvl"] == 1
mask

0     False
1     False
2      True
3      True
4      True
5     False
6      True
7     False
8      True
9     False
10    False
11     True
Name: ezlvl, dtype: bool

… then select the rows using the mask (Step 2).

players[mask]

	username	country	age	ezlvl	time	points	finished
2	emil	fr	52	1	324.61	1321	1
3	ivan	ca	50	1	39.51	226	0
4	hasan	tr	26	1	253.19	815	0
6	sanjay	ca	27	1	350.00	1401	1
8	shuo	cn	24	1	194.77	1043	0
11	joro	bg	22	1	381.97	1491	1

The above two step process can be combined into a more compact expression:

players[players["ezlvl"]==1]

	username	country	age	ezlvl	time	points	finished
2	emil	fr	52	1	324.61	1321	1
3	ivan	ca	50	1	39.51	226	0
4	hasan	tr	26	1	253.19	815	0
6	sanjay	ca	27	1	350.00	1401	1
8	shuo	cn	24	1	194.77	1043	0
11	joro	bg	22	1	381.97	1491	1

Sorting data frames

players.sort_values("time", ascending=False)

	username	country	age	ezlvl	time	points	finished
7	lena	uk	23	0	408.76	1745	1
11	joro	bg	22	1	381.97	1491	1
6	sanjay	ca	27	1	350.00	1401	1
1	jane	ca	21	0	331.64	1149	1
2	emil	fr	52	1	324.61	1321	1
10	anna	pl	18	0	303.66	1209	1
9	r0byn	us	59	0	255.55	1102	0
4	hasan	tr	26	1	253.19	815	0
8	shuo	cn	24	1	194.77	1043	0
0	mary	us	38	0	124.94	418	0
3	ivan	ca	50	1	39.51	226	0
5	jordan	us	45	0	28.49	206	0

Ranking (optional material)

We can also rank the players according to the time variable by using the method .rank() on the "time" column.

players["time"].rank(ascending=False)

0     10.0
1      4.0
2      5.0
3     11.0
4      8.0
5     12.0
6      3.0
7      1.0
8      9.0
9      7.0
10     6.0
11     2.0
Name: time, dtype: float64

The rank of an element in a list tells us the position it appears in when the list is sorted. We see from the players-ranked-by-time results that the player at index 7 has rank 1 (first), and the player at index 5 is ranked 12 (last).

Data visualization with Seaborn

The first step is to import the seaboarn module under the alias sns.

import seaborn as sns

All the Seaborn functions are now available under sns..

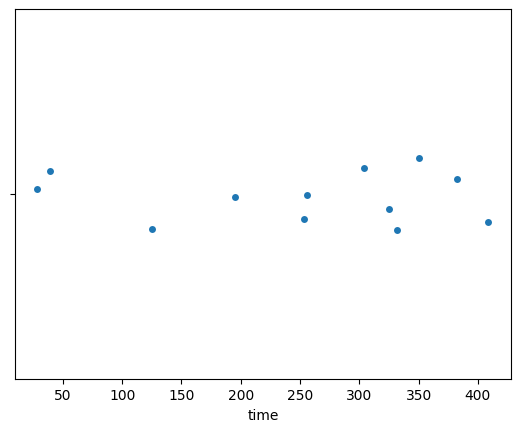
Strip plot of the time variable

To generate a strip plot, we pass the data frame players as the data argument to the Seaborn function sns.stripplot, and specify the column name "time" (in quotes) as the x argument.

sns.stripplot(data=players, x="time");

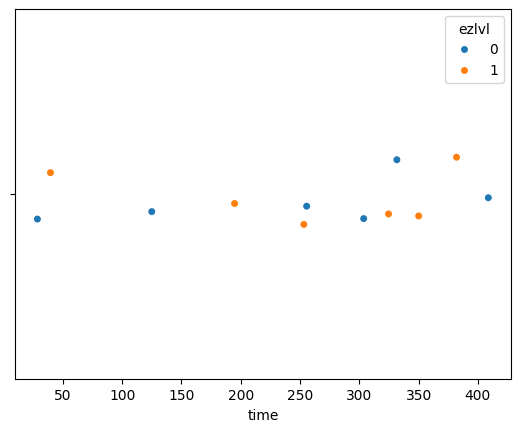
We can enhance the strip plot by mapping the ezlvl variable to the colour (hue) of the points in the plot.

sns.stripplot(data=players, x="time", hue="ezlvl");

Studying the effect of ezlvl on time

The players dataset was collected as part of an experiment designed to answer the question “Does the easy first level lead to an improvement in user retention?” We want to compare the time variable (total time players spent in the game) of players who were shown the “easy level” version of the game (ezlvl==1) to the control group of played who played the regular vesion of the game (ezlvl==0).

The mean time in the intervention group is:

mean1 = players[players["ezlvl"]==1]["time"].mean()
mean1

257.34166666666664

The mean time in the control group is:

mean0 = players[players["ezlvl"]==0]["time"].mean()
mean0

242.17333333333332

Let’s generate a strip plot of the time variable for the two groups of players.

sns.stripplot(data=players, x="time", y="ezlvl",
              hue="ezlvl", orient="h", legend=None);

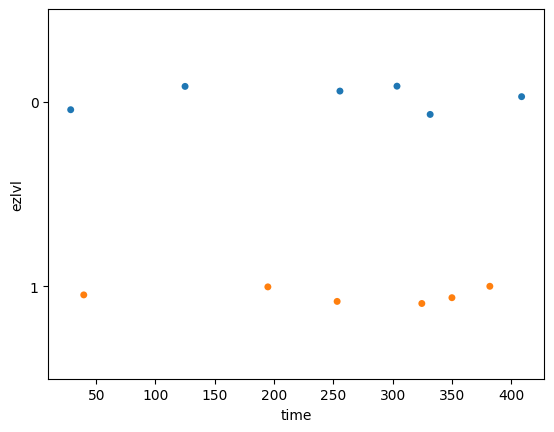
# # BONUS. stripplot with markers for the group means 
# sns.stripplot(data=players, x="time", y="ezlvl",
#               hue="ezlvl", orient="h", legend=None)
# sns.stripplot(x=[mean0], y=[0], marker="D", orient="h", color="b")
# sns.stripplot(x=[mean1], y=[1], marker="D", orient="h", color="r")

Studying the relationship between age and time

The secondary research question, is to look for a correlation between the age variable and the time variable.

sns.scatterplot(data=players, x="age", y="time");

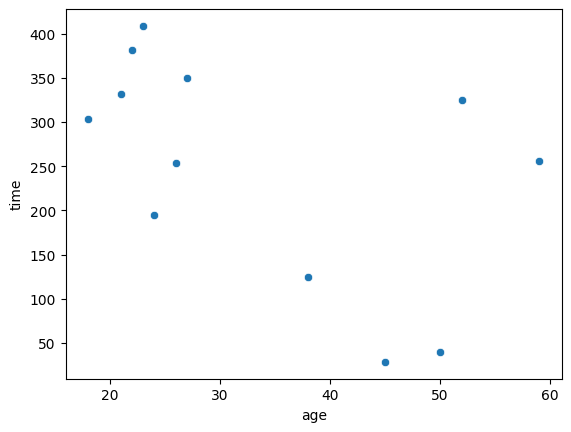
We can also create a linear regression plot using the regplot function.

sns.regplot(data=players, x="age", y="time", ci=None);

We’ll learn more about linear regression in Chapter 4.

Real-world datasets

Imagine you’re a data scientist consulting with various clients. Clients come to you with datasets and real-world questions they want to answer using statistical analysis. The following table shows the complete list of the datasets that we’ll use in examples and explanations in the rest of the book. The last column of the table tells us the sections of the book where each dataset will be discussed.

index	client name	filename	shape	sections
		players.csv	12x7	1.1, 1.2
1	Alice	apples.csv	30x1	3.1, 3.2
2	Bob	eprices.csv	18x2	3.1, 3.5
3	Charlotte	students.csv	15x5	1.3, 3.1, 3.5, 4.1
4	Khalid	kombucha.csv	347x2	3.1, 3.2, 3.3, 3.4
5	Dan	doctors.csv	157x12	3.1, 3.2, 3.5, 4.1
6	Vanessa	visitors.csv	2000x3	3.6
		minimal.csv	5x4	Appendix D

Let’s briefly describe the background story behind each dataset and state the statistical question that each client is interested in answering.

Apple weights

Alice runs an apple orchard. She collected a sample from the apples harvested this year (the population) and sent you the data in a CSV file called apples.csv.

You start by loading the data into Pandas and looking at its characteristics.

apples = pd.read_csv("../datasets/apples.csv")
apples.shape

(30, 1)

The first three observations in the apples dataset are:

apples.head(3)

	weight
0	205.0
1	182.0
2	192.0

The sample mean is:

apples['weight'].mean()

202.6

sns.stripplot(data=apples, x="weight", jitter=0, alpha=0.5);

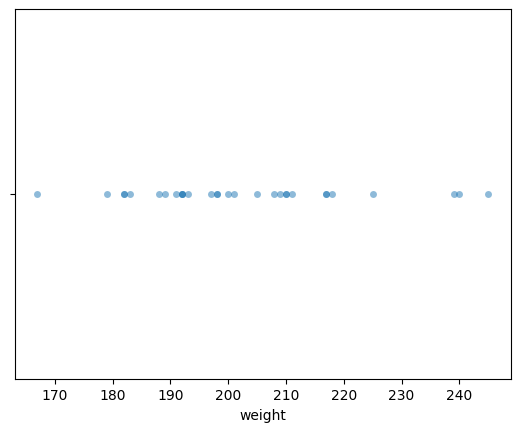
Electricity prices

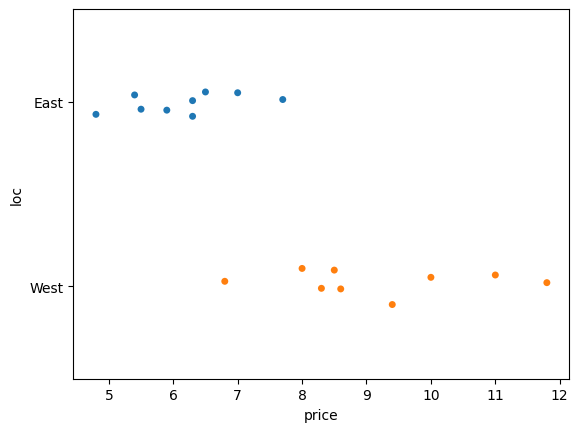
Bob recently bought an electric car. He doesn’t have a charging station for his car at home, so he goes to public charging stations to recharge the car’s batteries. Bob lives downtown, so he can go either to the East End or West End of the city for charging. He wants to know which side of the city has cheaper prices. Are electricity prices cheaper in the East End or the West End of the city?

To study this question, Bob collected electricity prices of East End and West End charging stations from a local price comparison website and provided you the prices in the dataset eprices.csv.

eprices = pd.read_csv("../datasets/eprices.csv")
eprices.shape

(18, 2)

The first three observations in the electricity prices dataset are:

eprices.head(3)

	loc	price
0	East	7.7
1	East	5.9
2	East	7.0

The average price in the West End is:

eprices[eprices["loc"]=="West"]["price"].mean()

9.155555555555557

The average price in the East End is:

eprices[eprices["loc"]=="East"]["price"].mean()

6.155555555555556

Let’s create a strip plot of electricity prices along the \(x\)-axis and use the loc variable to control the \(y\)-position and colour of the points.

sns.stripplot(data=eprices, x="price", y="loc", hue="loc");

Students’ scores

Charlotte is a science teacher who wants to test the effectiveness of a new teaching method in which material is presented in the form of a “scientific debate”. Student actors initially express “wrong” opinions, which are then corrected by presenting the “correct” way to think about science concepts. This type of teaching is in contrast to the usual lecture method, in which the teacher presents only the correct facts.

To compare the effectiveness of the two teaching methods, she has prepared two variants of her course:

• In the lecture variant, the video lessons present the material in the usual lecture format that includes only correct facts and explanations.

• In the debate variant, the same material is covered through video lessons in which student actors express multiple points of view, including common misconceptions.

Except for the different video lessons, the two variants of the course are identical: they cover the same topics, use the same total lecture time, and test students’ knowledge using the same assessment items.

Let’s load the data file students.csv into Pandas and see what it looks like.

students = pd.read_csv("../datasets/students.csv")
students.shape

(15, 5)

The first five observations in the students dataset are:

students.head()

	student_ID	background	curriculum	effort	score
0	1	arts	debate	10.96	75.0
1	2	science	lecture	8.69	75.0
2	3	arts	debate	8.60	67.0
3	4	arts	lecture	7.92	70.3
4	5	science	debate	9.90	76.1

We’re interested in comparing the two variants of the course, so we can generate a strip plot of the score variable, for the two groups defined by the curriculum variable.

sns.stripplot(data=students, x="score", y="curriculum", hue="curriculum");

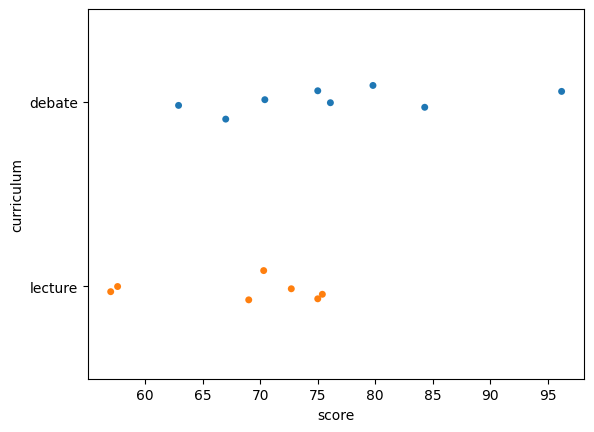
lstudents = students[students["curriculum"]=="lecture"]
lstudents["score"].mean()

68.14285714285714

dstudents = students[students["curriculum"]=="debate"]
dstudents["score"].mean()

76.4625

Kombucha volumes

Khalid is responsible for the production line at a kombucha brewing company. He needs to make sure the volume of kombucha that goes into each bottle is exactly 1 litre (1000 ml), but because of day-to-day variations in the fermentation process, production batches may end up with under-filled or over-filled bottles. Sending such irregular batches to clients will cause problems for the company, so Khalid wants to find a way to detect when the brewing and bottling process is not working as expected.

Khalid compiled the dataset kombucha.csv, which contains the volume measurements from samples taken from 10 different production batches,

kombucha = pd.read_csv("../datasets/kombucha.csv")
kombucha.shape

(347, 2)

kombucha.columns

Index(['batch', 'volume'], dtype='object')

The first three observations in the kombucha dataset are:

kombucha.head(3)

	batch	volume
0	1	1016.24
1	1	993.88
2	1	994.72

Let’s generate a combined strip plot of the observations from the different batches so that we can visually inspect the data.

sns.stripplot(data=kombucha, x="batch", y="volume", alpha=0.3);

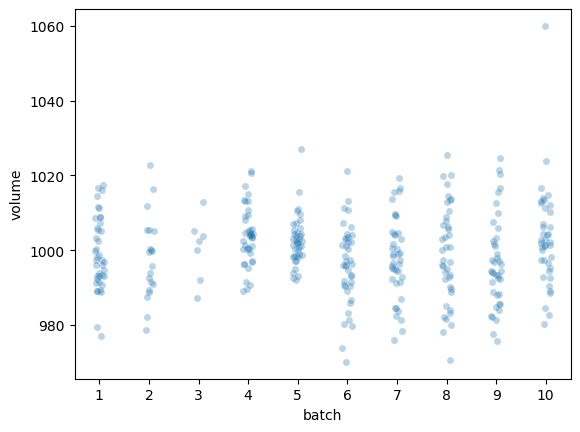
Average volume of the sample from Batch 01

batch01 = kombucha[kombucha["batch"]==1]
ksample01 = batch01["volume"]
ksample01.mean()

999.10375

Doctors’ sleep study

Dan is a data analyst working at the Ministry of Health. His current assignment is to look for ways to improve the health of family doctors. He collected the doctors dataset (doctors.csv), which contains data about the demographics, life habits, and health metrics of 224 family doctors that Dan randomly selected from the populations of family doctors in the country.

doctors = pd.read_csv("../datasets/doctors.csv")
doctors.shape

(156, 9)

The first three observations in the doctors dataset are:

doctors.head(3)

	permit	loc	work	hours	caf	alc	weed	exrc	score
0	93273	rur	hos	21	2	0	5.0	0.0	63
1	90852	urb	cli	74	26	20	0.0	4.5	16
2	92744	urb	hos	63	25	1	0.0	7.0	58

Dan is interested in comparing the sleep scores of doctors in rural and urban locations, so he starts by generating a strip plot of the score variable for the two values of the location variable.

sns.stripplot(data=doctors, x="score", y="loc", hue="loc");

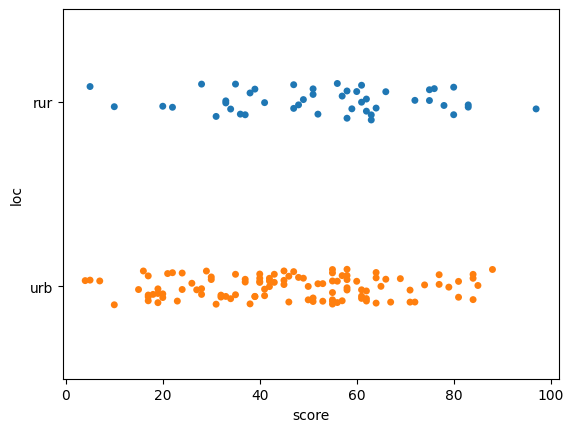
Average sleep scores for doctors in different locations

udoctors = doctors[doctors["loc"]=="urb"]
udoctors["score"].mean()

45.96363636363636

rdoctors = doctors[doctors["loc"]=="rur"]
rdoctors["score"].mean()

52.95652173913044

We see doctors in rural locations get better sleep, on average, than doctors in urban locations.

Website visitors

Vanessa runs an e-commerce website and is about to launch a new design for the homepage. She wants to know if the new design is better or worse than the current design. Vanessa has access to the server logs from her website and is able to collect data about which visitors clicked the BUY NOW button and bought something. The term conversion is used when a visitor buys something, meaning they are “converted” from visitor to client. The conversion rate is the proportion of website visitors that become clients.

Vanessa performed an experiment to check if the new website design is better than the current design when it comes to getting visitors to click the BUY NOW button. For the 2000 new visitors that the site received during the previous month, Vanessa randomly sent half of them to the new design (A for alternative), and the other half to the old design (B for baseline). She also recorded if a visitor bought a product during their visit to the website.

The data consists of 2000 observations from visitors to the website from unique IP addresses. For each visitor, the column version contains which design they were presented with, and the column bought records whether the visitor purchased something or not. You use the usual Pandas commands to load the dataset visitors.csv to inspect it.

visitors = pd.read_csv("../datasets/visitors.csv")
visitors.shape

(2000, 3)

The first five observations in the visitors dataset are:

visitors.head(5)

	IP address	version	bought
0	135.185.92.4	A	0
1	14.75.235.1	A	1
2	50.132.244.139	B	0
3	144.181.130.234	A	0
4	90.92.5.100	B	0

The average (mean) conversion rate for version A of the website is:

visitors[visitors["version"]=="A"]["bought"].mean()

0.06482465462274177

The average (mean) conversion rate for version B of the website is:

visitors[visitors["version"]=="B"]["bought"].mean()

0.03777148253068933

We can represent the two conversion rates using a bar plot.

sns.barplot(data=visitors, x="bought", y="version");

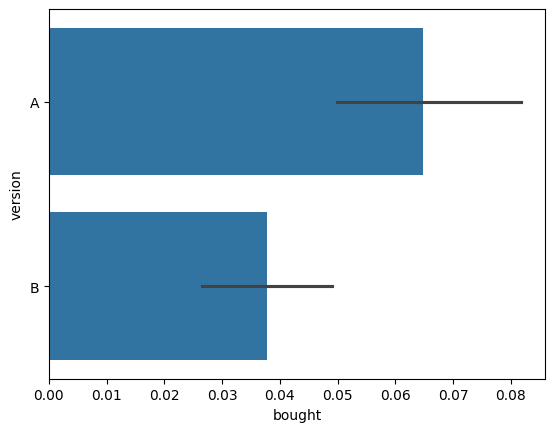
The black lines represent the estimates of the uncertainty of the true conversion rates that Seaborn automatically computed for us. Specifically, the black lines represent \(95\%\) confidence intervals for the true proportions. We’ll learn about confidence intervals later in the book (Section 3.2).

Discussion

Data extraction

See Appendix D: Pandas tutorial.

Data transformations

See Appendix D: Pandas tutorial.

Tidy data

epriceswide = pd.read_csv("../datasets/epriceswide.csv")
epriceswide.shape

(9, 2)

The data frame epriceswide is not tidy, because each row contains multiple observations.

epriceswide

	East	West
0	7.7	11.8
1	5.9	10.0
2	7.0	11.0
3	4.8	8.6
4	6.3	8.3
5	6.3	9.4
6	5.5	8.0
7	5.4	6.8
8	6.5	8.5

We can use the Pandas method .melt to convert the epriceswide data frame from “wide” format into “long” format, with one observation per row.

The method .melt takes the argument var_name to specify the name of the variable that is encoded in the column positions, and the argument value_name to specify the name of the variable stored in the individual cells.

epriceswide.melt(var_name="loc", value_name="price")

	loc	price
0	East	7.7
1	East	5.9
2	East	7.0
3	East	4.8
4	East	6.3
5	East	6.3
6	East	5.5
7	East	5.4
8	East	6.5
9	West	11.8
10	West	10.0
11	West	11.0
12	West	8.6
13	West	8.3
14	West	9.4
15	West	8.0
16	West	6.8
17	West	8.5

The .melt operation transformed the implicit “which column is the data in” information into an explicit loc variable stored in a separate column. Each row in the transformed data frame contains only a single observation, so it is in tidy data format.

The melted-epriceswide is the same as eprices dataset that we saw earlier. We can confirm this using the .equals method.

epriceslong = epriceswide.melt(var_name="loc", value_name="price")
eprices.equals(epriceslong)

True

Data cleaning

See Appendix D: Pandas tutorial.

Links

TODO: import from Appendix D