Section 5.3 — Bayesian linear models

Section 5.3 — Bayesian linear models#

This notebook contains the code examples from Section 5.3 Bayesian linear models from the No Bullshit Guide to Statistics.

Notebook setup#

# load Python modules
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Figures setup
plt.clf()  # needed otherwise `sns.set_theme` doesn"t work
from plot_helpers import RCPARAMS
# RCPARAMS.update({"figure.figsize": (9, 5)})   # good for screen
RCPARAMS.update({"figure.figsize": (6, 3)})  # good for print
sns.set_theme(
    context="paper",
    style="whitegrid",
    palette="colorblind",
    rc=RCPARAMS,
)

# High-resolution please
%config InlineBackend.figure_format = "retina"

#######################################################

<Figure size 640x480 with 0 Axes>

# set random seed for repeatability
np.random.seed(42)

# silence statsmodels kurtosistest warning when using n < 20
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
warnings.filterwarnings("ignore", category=FutureWarning)

Bayesian model#

TODO: formula

TODO: graphical model diagram

Example 1: students score as a function of effort#

Students dataset#

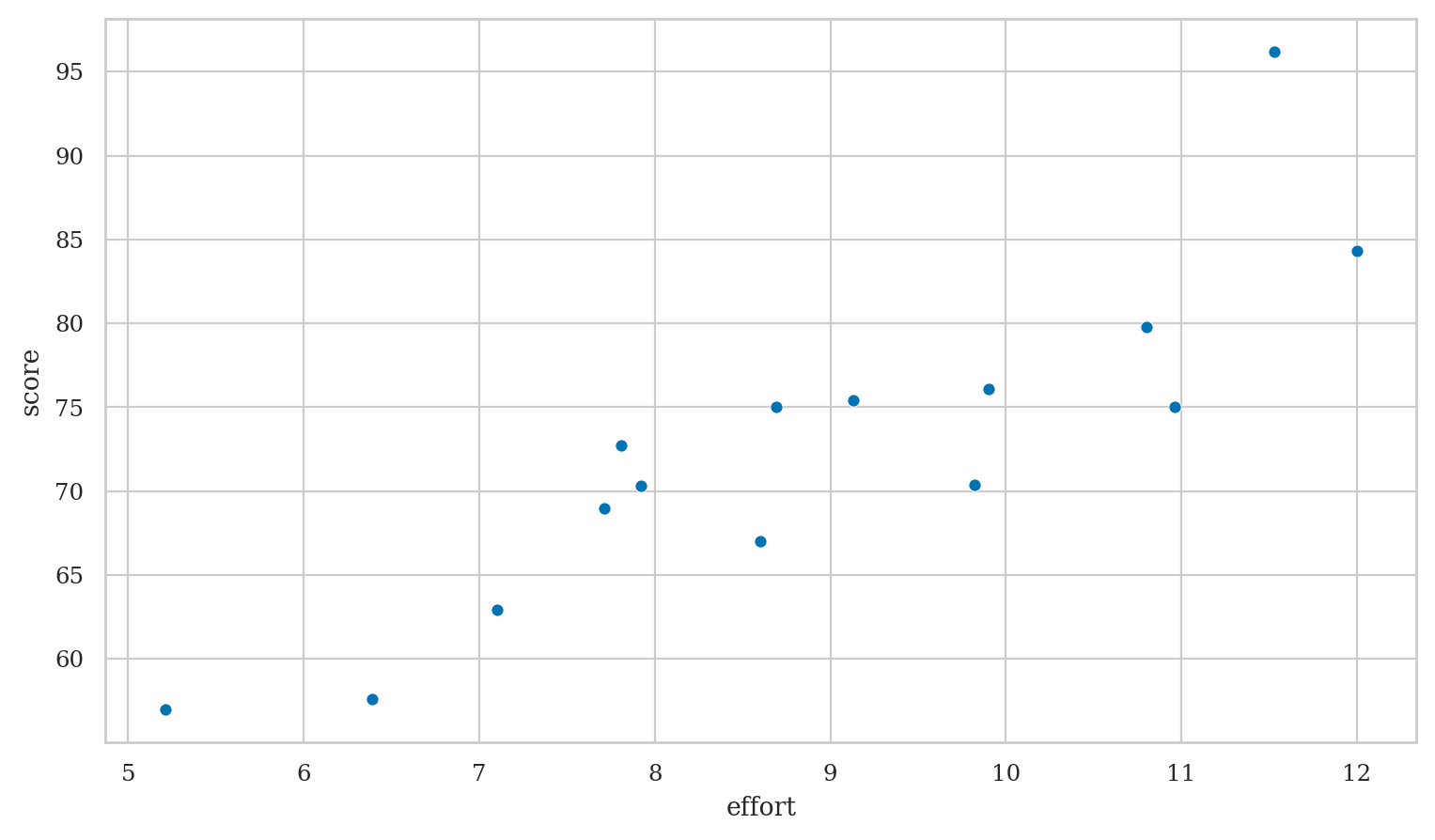
students = pd.read_csv("../datasets/students.csv")
students.shape

(15, 5)

students.head(3)

	student_ID	background	curriculum	effort	score
0	1	arts	debate	10.96	75.0
1	2	science	lecture	8.69	75.0
2	3	arts	debate	8.60	67.0

students[["effort","score"]].describe().T

	count	mean	std	min	25%	50%	75%	max
effort	15.0	8.904667	1.948156	5.21	7.76	8.69	10.35	12.0
score	15.0	72.580000	9.979279	57.00	68.00	72.70	75.75	96.2

sns.scatterplot(x="effort", y="score", data=students);

../_images/f2c19677424f89dfaf13d95c97d38e1bea5328709561f580f1e7be5118c28f21.png

Bayesian model#

TODO: add formulas

Bambi model#

import bambi as bmb

priors1 = {
    "Intercept": bmb.Prior("Normal", mu=70, sigma=20),
    "effort": bmb.Prior("Normal", mu=0, sigma=10),
    "sigma": bmb.Prior("HalfStudentT", nu=4, sigma=10),
}

mod1 = bmb.Model("score ~ 1 + effort",
                 family="gaussian",
                 link="identity",
                 priors=priors1,
                 data=students)

Inspecting the Bambi model#

mod1

       Formula: score ~ 1 + effort
        Family: gaussian
          Link: mu = identity
  Observations: 15
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 70.0, sigma: 20.0)
            effort ~ Normal(mu: 0.0, sigma: 10.0)
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 10.0)

mod1.build()
mod1.graph()

../_images/b906c538290ee972afc2fbcc8a2a14e7ff0c3ea5f1c0d10d9a81214490f11ac7.svg

Prior predictive checks#

# TODO

Model fitting and analysis#

idata1 = mod1.fit(random_seed=[42,42,44,45])

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [sigma, Intercept, effort]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 2 seconds.

We recommend running at least 4 chains for robust computation of convergence diagnostics

import arviz as az
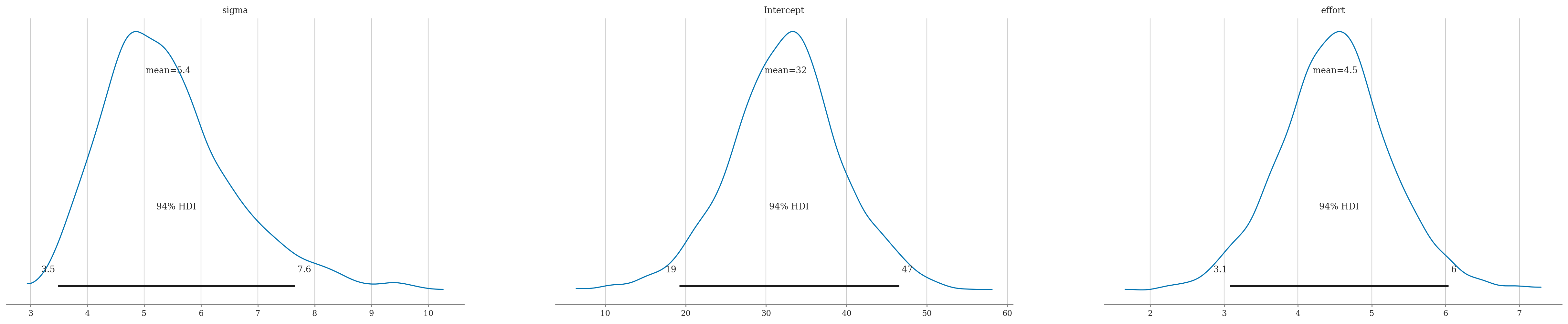
az.summary(idata1, kind="stats")

	mean	sd	hdi_3%	hdi_97%
sigma	5.381	1.182	3.343	7.347
Intercept	32.857	6.933	20.293	45.224
effort	4.461	0.768	3.050	5.876

az.plot_posterior(idata1);

../_images/aee42059f2a718d59b134fa1c62cc057d0e4c06ac9243027260b5b90724914cc.png

Model predictions#

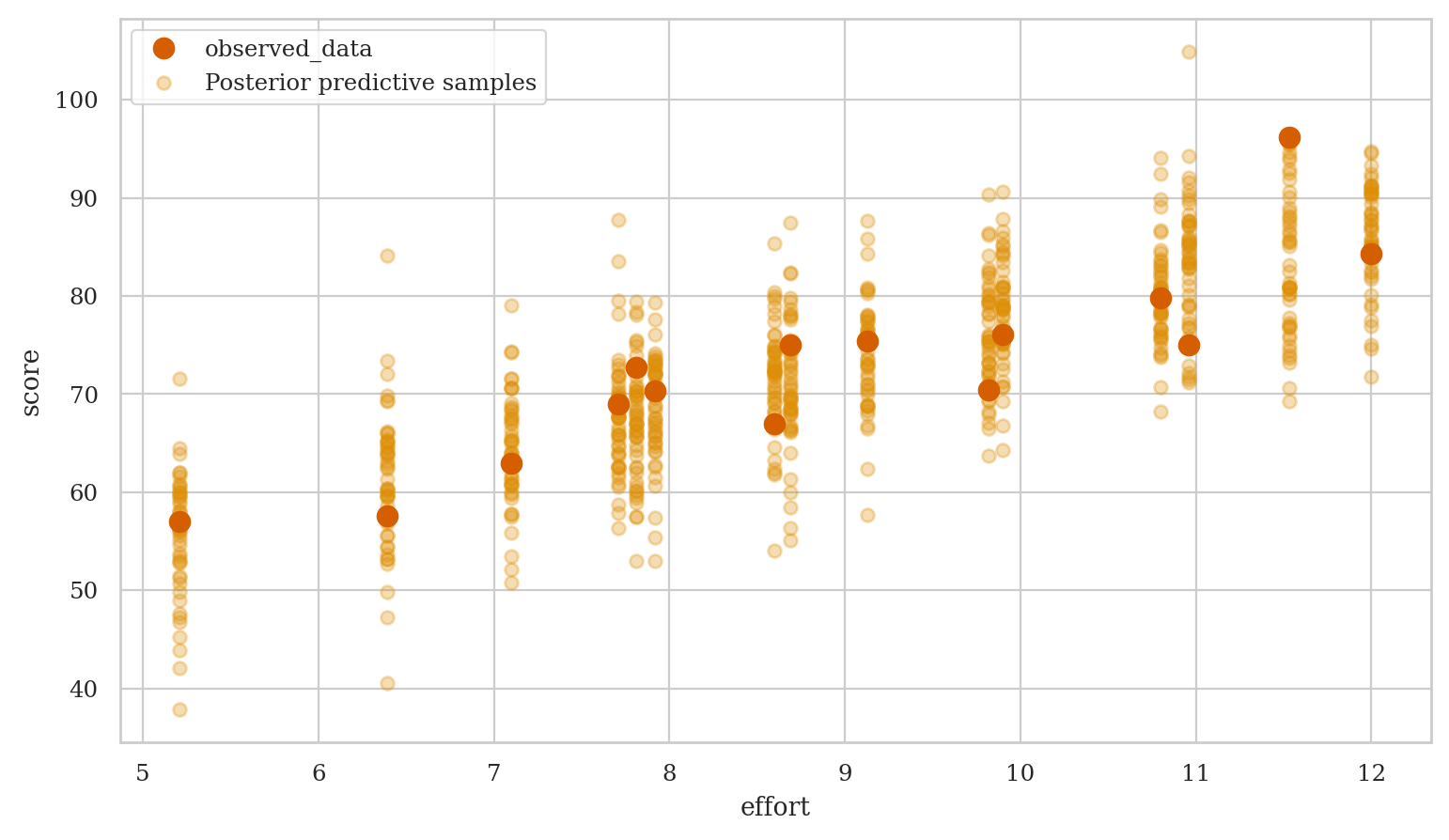
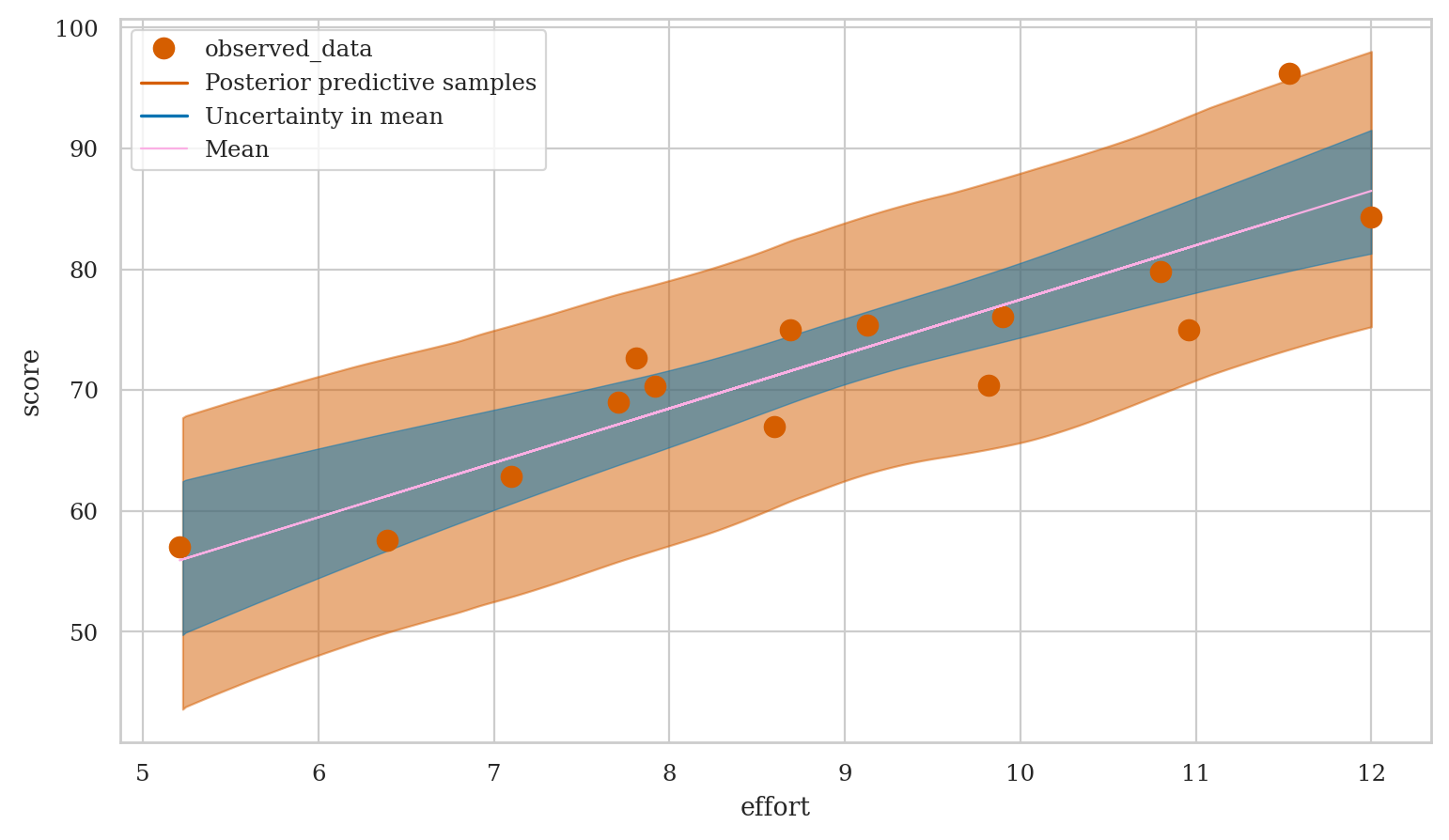
Generate samples form the posterior predictive distribution, then use the ArviZ function plot_lm to generate a complete visualization.

preds1 = mod1.predict(idata=idata1, data=students,
                      kind="response", inplace=False)
efforts = students["effort"]
az.plot_lm(y="score", idata=preds1, x=efforts,
           y_model="mu", y_hat="score",
           kind_pp="samples", kind_model="lines");

../_images/b391c812fbb547970553e610d871618cd50fbfc060692b6809896f09cd85007d.png

az.plot_lm(y="score", idata=preds1, x=efforts,
           y_model="mu", y_hat="score",
           kind_pp="hdi", kind_model="hdi");

../_images/a04e8ff5a23b8bdbfbeb13ab36f67f5ba354cb93765051c8831a213fdf697d99.png

Comparing to frequentist results#

For your convenience, I’ll reproduce the statsmodels analysis from Section 4.1.

# compare with statsmodels results
import statsmodels.formula.api as smf
lm1 = smf.ols("score ~ 1 + effort", data=students).fit()
lm1.summary().tables[1]

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	32.4658	6.155	5.275	0.000	19.169	45.763
effort	4.5049	0.676	6.661	0.000	3.044	5.966

np.sqrt(lm1.scale)

4.929598282660258

lm1.conf_int(alpha=0.06)  # to match 94% coverage of the Bayesian HDIs

	0	1
Intercept	19.786169	45.145449
effort	3.111697	5.898004

Conclusions#

We see effort tends to increase student scores. The results we obtain from the Bayesian analysis are largely consistent with the frequentist results from Section 4.1, however Bayesian models allow for simpler interpretation.

Example 2: doctors sleep scores#

Doctors dataset#

doctors = pd.read_csv("../datasets/doctors.csv")
doctors.shape

(156, 9)

doctors.head(3)

	permit	loc	work	hours	caf	alc	weed	exrc	score
0	93273	rur	hos	21	2	0	5.0	0.0	63
1	90852	urb	cli	74	26	20	0.0	4.5	16
2	92744	urb	hos	63	25	1	0.0	7.0	58

doctors[["alc","weed","exrc","score"]].describe().T

	count	mean	std	min	25%	50%	75%	max
alc	156.0	11.839744	9.428506	0.0	3.750	11.0	19.0	44.0
weed	156.0	0.628205	1.391068	0.0	0.000	0.0	0.5	10.5
exrc	156.0	5.387821	4.796361	0.0	0.875	4.5	8.0	19.0
score	156.0	48.025641	20.446294	4.0	33.000	49.5	62.0	97.0

Bayesian model#

TODO: add formulas

Bambi model#

priors2 = {
    "Intercept": bmb.Prior("Normal", mu=50, sigma=40),
    # we'll set the priors for the slopes below
    "sigma": bmb.Prior("HalfStudentT", nu=4, sigma=20),
}

mod2 = bmb.Model("score ~ 1 + alc + weed + exrc",
                 family="gaussian",
                 link="identity",
                 priors=priors2,
                 data=doctors)

# set the same prior for all slopes using `set_priors`
slope_prior = bmb.Prior("Normal", mu=0, sigma=10)
mod2.set_priors(common=slope_prior)

mod2

       Formula: score ~ 1 + alc + weed + exrc
        Family: gaussian
          Link: mu = identity
  Observations: 156
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 50.0, sigma: 40.0)
            alc ~ Normal(mu: 0.0, sigma: 10.0)
            weed ~ Normal(mu: 0.0, sigma: 10.0)
            exrc ~ Normal(mu: 0.0, sigma: 10.0)
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 20.0)

mod2.build()
mod2.graph()

../_images/741828b363ea7735de4120e2b5f0be21f3ac11a72a5a4cee6930e2f9c8e0abb8.svg

Prior predictive checks#

What kind of parameters (lines) do we get from the data model when the distribution of the parameters comes from random samples from the priors?

# TODO

Model fitting and analysis#

idata2 = mod2.fit(random_seed=[42,43,44,45])

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [sigma, Intercept, alc, weed, exrc]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 2 seconds.

We recommend running at least 4 chains for robust computation of convergence diagnostics

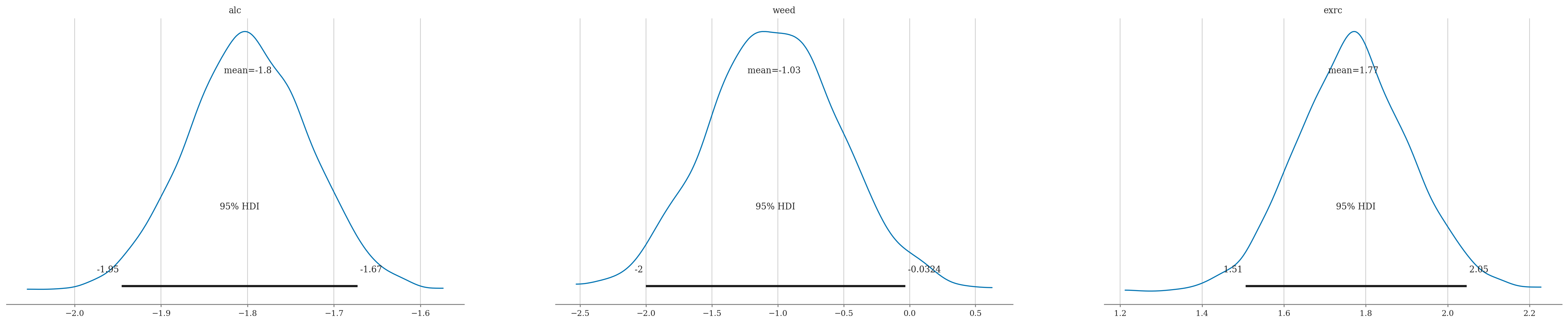
az.summary(idata2, kind="stats", hdi_prob=0.95)

	mean	sd	hdi_2.5%	hdi_97.5%
sigma	8.270	0.478	7.327	9.171
Intercept	60.420	1.266	58.166	62.989
alc	-1.798	0.071	-1.931	-1.653
weed	-1.014	0.498	-2.044	-0.115
exrc	1.766	0.138	1.512	2.047

az.plot_posterior(idata2, hdi_prob=0.95, round_to=3,
                  var_names=["alc", "weed", "exrc"]);

../_images/9daffabe47233ce60acf673a1e55a4862cee83b382f27d30822cef8f67701793.png

Partial correlation scale?#

cf. https://bambinos.github.io/bambi/notebooks/ESCS_multiple_regression.html#summarize-effects-on-partial-correlation-scale

Comparing to frequentist results#

For your convenience, I’ll reproduce the statsmodels analysis from Section 4.2.

# compare with statsmodels results
import statsmodels.formula.api as smf
formula = "score ~ 1 + alc + weed + exrc"
lm2 = smf.ols(formula, data=doctors).fit()
lm2.summary().tables[1]

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	60.4529	1.289	46.885	0.000	57.905	63.000
alc	-1.8001	0.070	-25.726	0.000	-1.938	-1.662
weed	-1.0216	0.476	-2.145	0.034	-1.962	-0.081
exrc	1.7683	0.138	12.809	0.000	1.496	2.041

np.sqrt(lm2.scale)

8.202768119825624

Conclusions#

Example 3: Bayesian logistic regression#

Interns data#

interns = pd.read_csv("../datasets/interns.csv")
interns.head(3)

	work	hired
0	42.5	1
1	39.3	0
2	43.2	1

Bayesian logistic regression model#

Bambi model#

priors3 = {
    "Intercept": bmb.Prior("Normal", mu=0, sigma=20),
    "work": bmb.Prior("Normal", mu=2, sigma=2),
}

mod3 = bmb.Model("hired ~ 1 + work",
                 family="bernoulli",
                 link="logit",
                 priors=priors3,
                 data=interns)
mod3

       Formula: hired ~ 1 + work
        Family: bernoulli
          Link: p = logit
  Observations: 100
        Priors: 
    target = p
        Common-level effects
            Intercept ~ Normal(mu: 0.0, sigma: 20.0)
            work ~ Normal(mu: 2.0, sigma: 2.0)

mod3.build()
mod3.graph()

../_images/76dfafdb85bb98a4cd56b96f2df79fd0dc1d8493180231e585f8318cd797f8ba.svg

Prior predictive checks#

# # TODO: improve prior predictive plot (currently runs too slowly)
# idatapp = mod3.prior_predictive()
# for i in range(300):
#     ps = idatapp["prior"].sel(draw=[i], chain=[0])["p"].values.flatten()
#     ws = interns["work"]
#     sps = ps[ws.sort_values().index]
#     sws = ws.sort_values().values
#     sns.lineplot(x=sws, y=sps, alpha=0.2)

Model fitting and analysis#

idata3 = mod3.fit(random_seed=[42,43,44,45])

Modeling the probability that hired==1

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [Intercept, work]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 1 seconds.

We recommend running at least 4 chains for robust computation of convergence diagnostics

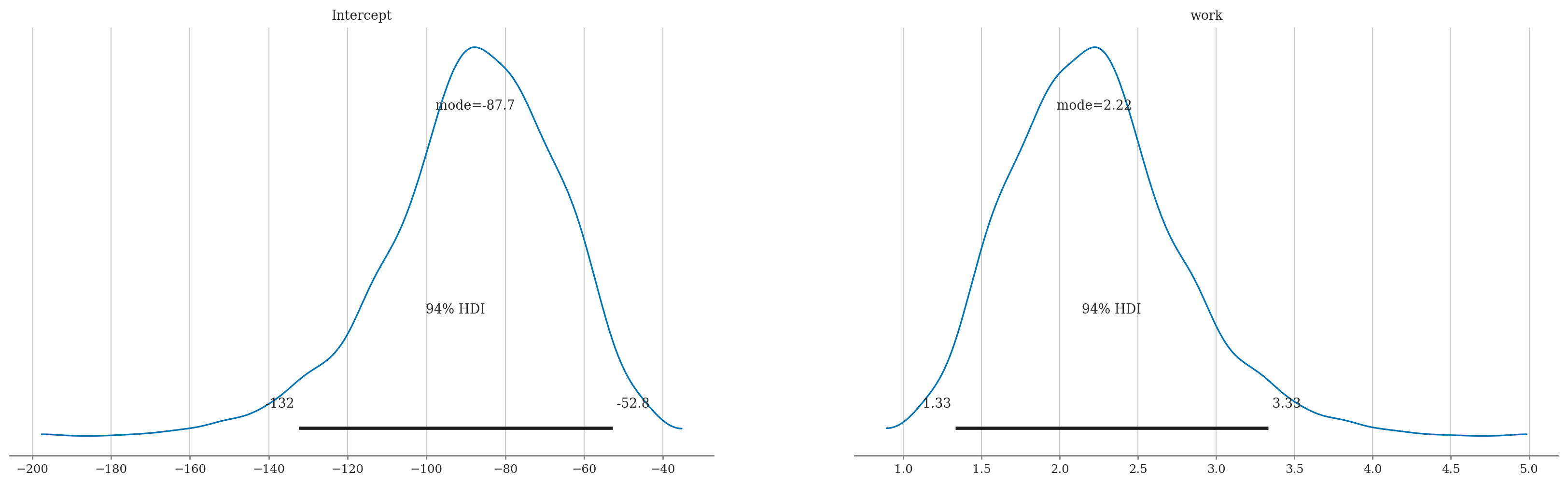
az.summary(idata3, kind="stats")

	mean	sd	hdi_3%	hdi_97%
Intercept	-88.113	22.323	-129.907	-47.384
work	2.219	0.563	1.291	3.372

az.plot_posterior(idata3, round_to=3, point_estimate="mode");

../_images/c9b7fb38b6992a597789e723a94bdf0209c01d87addc959ced7649a5adff0bc9.png

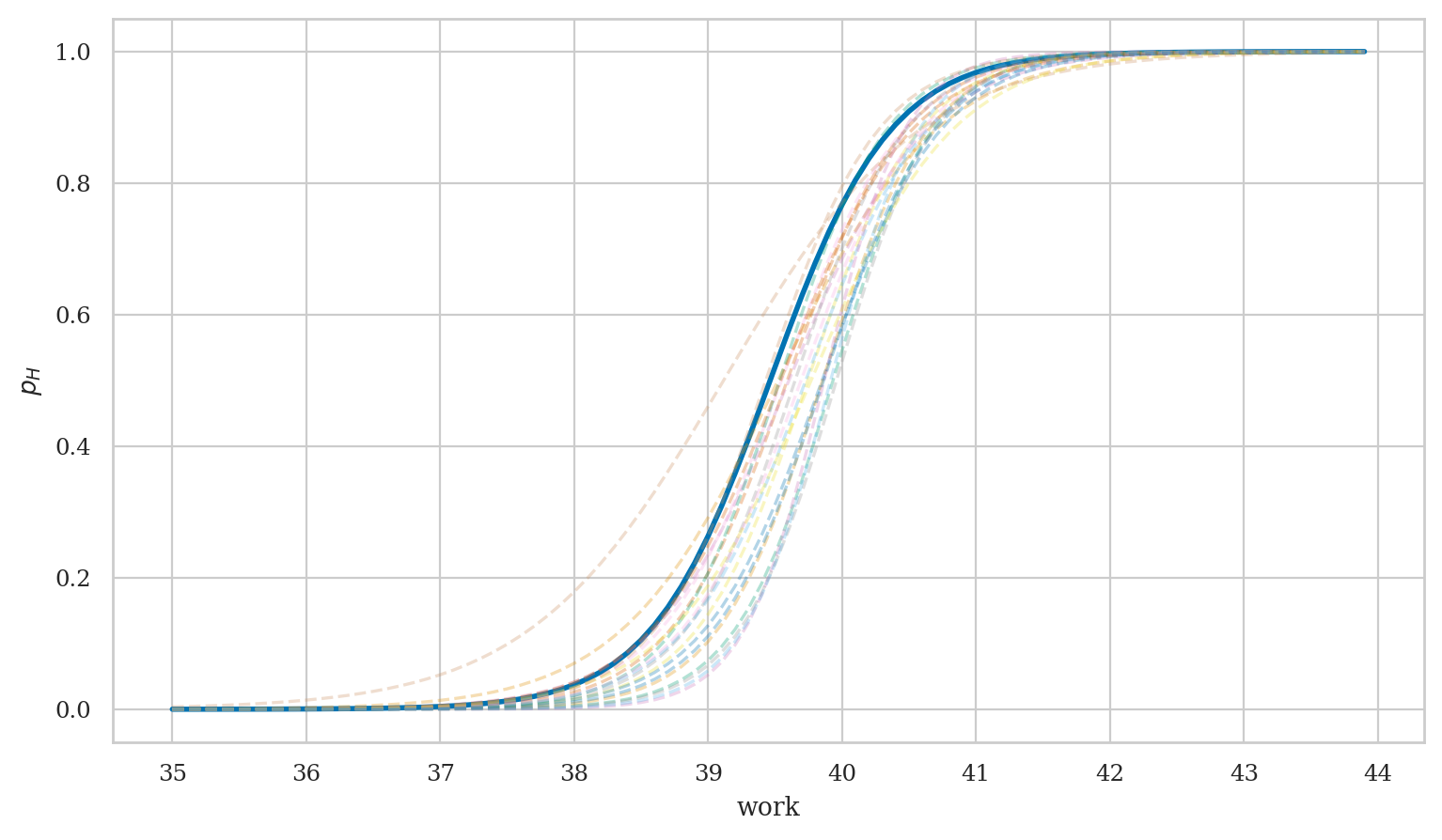
Visualize variability of the results#

from scipy.special import expit

# generate predictions
works = np.arange(35, 44, 0.1)
new_interns = pd.DataFrame({"work": works})
idata3_pred = mod3.predict(idata3, data=new_interns, inplace=False)

# plot best-fit curve based on MAP estimates
intercepts = idata3["posterior"]['Intercept'].values
wslopes = idata3["posterior"]['work'].values
B0_MAP = az.plots.plot_utils.calculate_point_estimate('mode', intercepts)
Bw_MAP = az.plots.plot_utils.calculate_point_estimate('mode', wslopes)
print("MAP estimates:", B0_MAP.round(1), Bw_MAP.round(2))
p_MAP = expit(B0_MAP + Bw_MAP*works)
ax = sns.lineplot(x=works, y=p_MAP, lw=2)

# plot 40 samples
subset = np.random.choice(1000, 10, replace=False)
post3 = idata3_pred["posterior"]
post3_subset = post3.sel(draw=subset)
for ps in az.extract(post3_subset, var_names="p").T:
    sns.lineplot(x=works, y=ps, alpha=0.3, ax=ax, ls="--")
ax.set_xlabel("work")
ax.set_ylabel("$p_H$")
ax.set_xticks(range(35,44+1));

MAP estimates: -82.0 2.04

../_images/32c4bbc1e69b5bcb527181b8a621376305ee795a5626ea349afd91ff3823d8cb.png

Interpretation of the parameters#

We can interpret the results on the log-odds scale, the odds scale, or as marginal effects (slopes) at particular values of the predictor \(w\).

Parameters as changes in the log-odds#

The mode of the posterior distribution \(\widehat{B_w}_{\text{MAP}}\) corresponds to the change in log-odds per unit increase in work hours.

from ministats import mode_from_samples

post_work = idata3["posterior"]["work"].values.flatten()
mode_from_samples(post_work)

2.056171122976707

Parameters as ratios of odds#

We can also \tt{exp}-transform this estimate to obtain the rate of increase in the odds of getting hired per additional hour of work invested.

np.exp(2.01)

7.463317347319193

Actually, the more accurate way to summarize the odds ratio would be to exp-transform the whole posterior distribution \(f_{B_w|\tt{interns}}\), then find the maximum using mode_from_samples(np.exp(post_work)), which produces the estimate \(6.81\).

Differences in probabilities#

What is the marginal effect of the predictor work for an intern who invests 40 hours of effort?

bmb.interpret.slopes(mod3, idata3, wrt={"work":[40]}, average_by=True)

	term	estimate_type	estimate	lower_3.0%	upper_97.0%
0	work	dydx	0.469456	0.266966	0.727226

# ALT. manual calculation based on derivative of `expit`
# sample the parameter p from `mod3` when work=40
work40 = pd.DataFrame({"work": [40]})
preds = mod3.predict(idata3, data=work40, inplace=False)
ps40 = preds["posterior"]["p"].values.flatten()
# use the slope formula dp/dwork = p*(1-p)*beta_work
marg_effect_at_40 = ps40 * (1 - ps40) * post_work
marg_effect_at_40.mean()

0.46947133148444914

Predictions#

Let’s use the logistic regression model mod3 to predict the probability of being hired for an intern that invests 42 hours of work per week.

work42 = pd.DataFrame({"work": [42]})
preds42 = mod3.predict(idata3, data=work42, inplace=False)
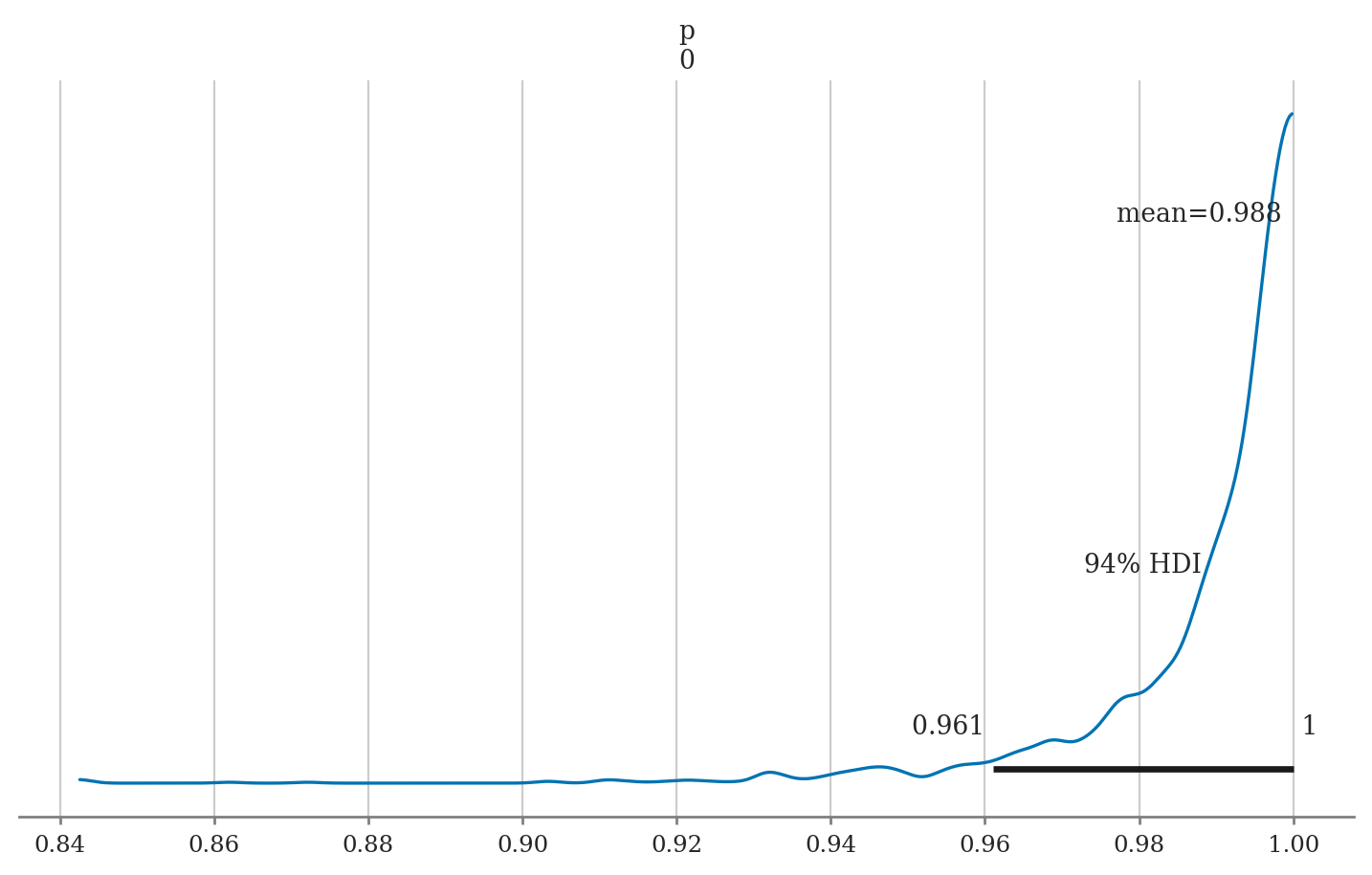
print(az.summary(preds42, var_names="p", kind="stats"))

       mean     sd  hdi_3%  hdi_97%
p[0]  0.987  0.017   0.957      1.0

The mean model prediction is \(p(42) = 0.987 = 98.7\%\), with \(\mathbf{hdi}_{p,0.94} = [0.959, 1.0]\), which means the intern will very likely get hired.

# ALT. compute using Bambi helper function
bmb.interpret.predictions(mod3, idata3, conditional={"work":42})

	work	estimate	lower_3.0%	upper_97.0%
0	42.0	0.98698	0.957097	0.999994

Plot predictions#

We can visualize the predictions by plotting a histogram.

az.plot_posterior(preds42, var_names="p", round_to=3);

../_images/0d883b41ab2e579da3180f7d43172d96f530352bdbe23c5226ca209985c6ae90.png

Comparing to frequentist results#

For your convenience, I’ll reproduce the statsmodels analysis from Section 4.6.

import statsmodels.formula.api as smf
lr1 = smf.logit("hired ~ 1 + work", data=interns).fit()
lr1.params

Optimization terminated successfully.
         Current function value: 0.138101
         Iterations 10

Intercept   -78.693205
work          1.981458
dtype: float64

lr1.conf_int(alpha=0.06)

	0	1
Intercept	-116.028234	-41.358176
work	1.040205	2.922711

Conclusions#

We end up with similar results…

Explanations#

Robust linear regression#

We swap out the Normal distribution for Student’s \(t\)-distribution to handle outliers better very useful when data has outliers; see EXX

Links:

#######################################################
priors1r = {
    "Intercept": bmb.Prior("Normal", mu=70, sigma=20),
    "effort": bmb.Prior("Normal", mu=0, sigma=10),
    "sigma": bmb.Prior("HalfStudentT", nu=4, sigma=10),
    "nu": bmb.Prior("Gamma", alpha=2, beta=0.1),
}

mod1r = bmb.Model("score ~ 1 + effort",
                 family="t",
                 link="identity",
                 priors=priors1r,
                 data=students)
mod1r

       Formula: score ~ 1 + effort
        Family: t
          Link: mu = identity
  Observations: 15
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 70.0, sigma: 20.0)
            effort ~ Normal(mu: 0.0, sigma: 10.0)
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 10.0)
            nu ~ Gamma(alpha: 2.0, beta: 0.1)

idata1r = mod1r.fit(random_seed=[42,43,44,45])

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [sigma, nu, Intercept, effort]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 2 seconds.

We recommend running at least 4 chains for robust computation of convergence diagnostics

print(az.summary(idata1r, kind="stats"))

             mean      sd  hdi_3%  hdi_97%
sigma       4.860   1.229   2.855    7.239
nu         18.859  13.211   1.427   43.036
Intercept  34.285   6.350  22.623   46.894
effort      4.274   0.724   2.933    5.701

The mean of the slope \(4.303\) is slightly less than the mean slope we found in mod1 (\(4.497\)), which shows the robust model doesn’t care as much about the one outlier.

We also found a slightly smaller sigma, since we’re using the \(t\)-distribution.

Shrinkage priors#

Shrinkage priors = Prior distributions for a parameter that shrink its posterior estimate towards a particular value. Sparsity = A situation where most parameter values are zero and only a few are non-zero.

Laplace priors L1 regularization = lasso regression https://en.wikipedia.org/wiki/Lasso_(statistics)
Gaussian priors L2 regularization = ridge regression https://en.wikipedia.org/wiki/Ridge_regression
Reference priors Reference prior ppal pha, beta, sigmaq91{sigma Produces the same results as frequentist linear regression
Spike-and-slab priors Specialized for spike-and-slab prior = mix- ture of two distributions: one peaked around zero (spike) and the other a diffuse distribution (slab. The spike component identifies the zero elements whereas the slab component captures the non-zero coefficients.

Standardizing predictors#

We make choosing priors easier makes inference more efficient cf. 04_lm/cut_material/standardized_predictors.tex Robust linear regression

Discussion#

Comparison to frequentist linear models#

We can obtain similar results
Bayesian models naturally apply regularization (no need to manually add in)

Causal graphs#

Causal graphs also used with Bayesian LMs (remember Sec 4.5)

Next steps#

LMs work with categorical predators too, which is what we’ll discuss in Section 5.4
LMs can be extended hierarchical models, which is what we’ll discuss in Section 5.5

Exercises#

Exercise 1: redo some of the exercises/problems from Ch4 using Bayesian methods#

Exercise 2: redo examples of causal inference#

Exercise 3: fit model with different priors#

Exercise 4: redo logistic regression exercises from Sec 4.6#

Exercise 5: bioassay logistic regression#

Gelman et al. (2003) present an example of an acute toxicity test, commonly performed on animals to estimate the toxicity of various compounds.

In this dataset log_dose includes 4 levels of dosage, on the log scale, each administered to 5 rats during the experiment. The response variable is death, the number of positive responses to the dosage.

The number of deaths can be modeled as a binomial response, with the probability of death being a linear function of dose:

\[\begin{split}\begin{aligned} y_i &\sim \text{Binom}(n_i, p_i) \\ \text{logit}(p_i) &= a + b x_i \end{aligned}\end{split}\]

The common statistic of interest in such experiments is the LD50, the dosage at which the probability of death is 50%.

via fonnesbeck/pymc_sdss_2024

# Sample size in each group
n = 5

# Log dose in each group
log_dose = [-.86, -.3, -.05, .73]

# Outcomes
deaths = [0, 1, 3, 5]

df_bio = pd.DataFrame({"log_dose":log_dose, "deaths":deaths, "n":n})

# SOLUTION
priors_bio = {
    "Intercept": bmb.Prior("Normal", mu=0, sigma=5),
    "log_dose": bmb.Prior("Normal", mu=0, sigma=5),
}

mod_bio = bmb.Model(formula="p(deaths,n) ~ 1 + log_dose",
                    family="binomial",
                    link="logit",
                    priors=priors_bio,
                    data=df_bio)

idata_bio = mod_bio.fit()

post_bio = idata_bio["posterior"]
post_bio["LD50"] = -post_bio["Intercept"] / post_bio["log_dose"]

az.summary(idata_bio)

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [Intercept, log_dose]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 1 seconds.

We recommend running at least 4 chains for robust computation of convergence diagnostics

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
Intercept	0.647	0.820	-0.869	2.165	0.024	0.020	1234.0	1175.0	1.0
log_dose	6.496	2.568	2.320	11.436	0.080	0.070	1189.0	909.0	1.0
LD50	-0.089	0.135	-0.325	0.181	0.004	0.004	1221.0	1247.0	1.0

Exercise 6: redo Poisson regression exercises from Sec 4.6#

Exercise 7: fit normal and robust to the dataset ??TODO?? which has outliers#

Exercise 8: PhD delays#

cf. https://www.rensvandeschoot.com/tutorials/advanced-bayesian-regression-in-jasp/
https://zenodo.org/records/3999424
https://sci-hub.se/https://www.nature.com/articles/ s43586-020-00001-2

Links#

BONUS MATERIAL#

Simple linear regression using PyMC#

(used in Chapter 4 conclusion)

# Linear regression model in PyMC
students = pd.read_csv("../datasets/students.csv")

import pymc as pm
with pm.Model() as model:
    # Define the priors
    B0 = pm.Normal("B0", mu=30, sigma=20)
    Be = pm.Normal("Be", mu=0, sigma=10)
    Sigma = pm.HalfStudentT("Sigma", nu=4, sigma=10)
    
    # Define the data model
    M = B0 + Be * students["effort"]
    S = pm.Normal("S", mu=M, sigma=Sigma, observed=students["score"])
    
    # Fit the model
    idata = pm.sample()

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [B0, Be, Sigma]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 3 seconds.

There were 2 divergences after tuning. Increase `target_accept` or reparameterize.

We recommend running at least 4 chains for robust computation of convergence diagnostics

import arviz as az
az.summary(idata, kind="stats")

	mean	sd	hdi_3%	hdi_97%
B0	32.633	6.175	20.514	44.154
Be	4.485	0.674	3.256	5.843
Sigma	5.366	1.162	3.592	7.577

# cf. with Bambi results for the same model
az.summary(idata1, kind="stats")

	mean	sd	hdi_3%	hdi_97%
sigma	5.381	1.182	3.343	7.347
Intercept	32.857	6.933	20.293	45.224
effort	4.461	0.768	3.050	5.876

Simple linear regression on synthetic data#

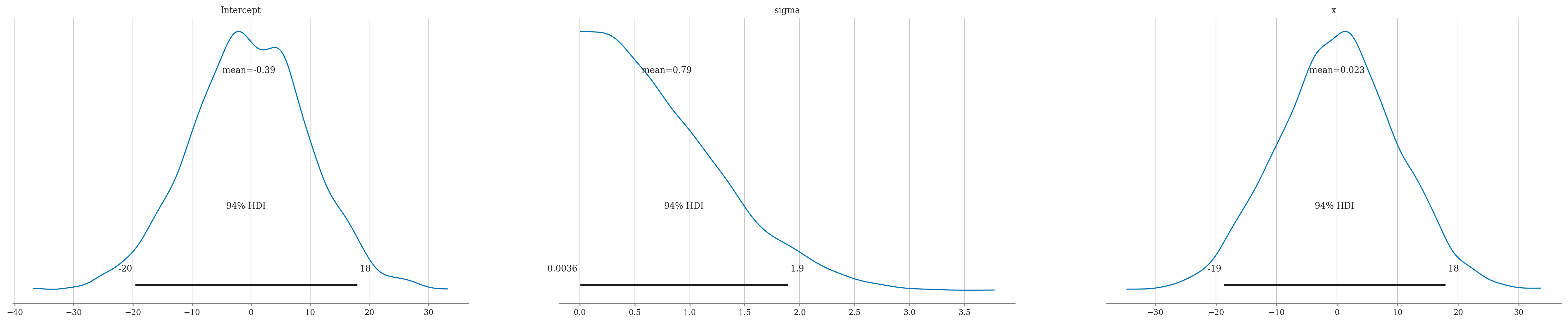
# Simulated data
np.random.seed(42)
x = np.random.normal(0, 1, 100)
y = 3 + 2 * x + np.random.normal(0, 1, 100)

df1 = pd.DataFrame({"x":x, "y":y})

priors1 = {
    "Intercept": bmb.Prior("Normal", mu=0, sigma=10),
    "x": bmb.Prior("Normal", mu=0, sigma=10),
    "sigma": bmb.Prior("HalfNormal", sigma=1),
}

model1 = bmb.Model("y ~ 1 + x",
                   priors=priors1,
                   data=df1)
print(model1)

idata = model1.fit()

Initializing NUTS using jitter+adapt_diag...

       Formula: y ~ 1 + x
        Family: gaussian
          Link: mu = identity
  Observations: 100
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 0.0, sigma: 10.0)
            x ~ Normal(mu: 0.0, sigma: 10.0)
        
        Auxiliary parameters
            sigma ~ HalfNormal(sigma: 1.0)

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [sigma, Intercept, x]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 1 seconds.

We recommend running at least 4 chains for robust computation of convergence diagnostics

model1.plot_priors();

Sampling: [Intercept, sigma, x]

../_images/8a0cdc78f1d04a156da7e3969ffca050c3407e7658c976e7d371bb3b3232c876.png

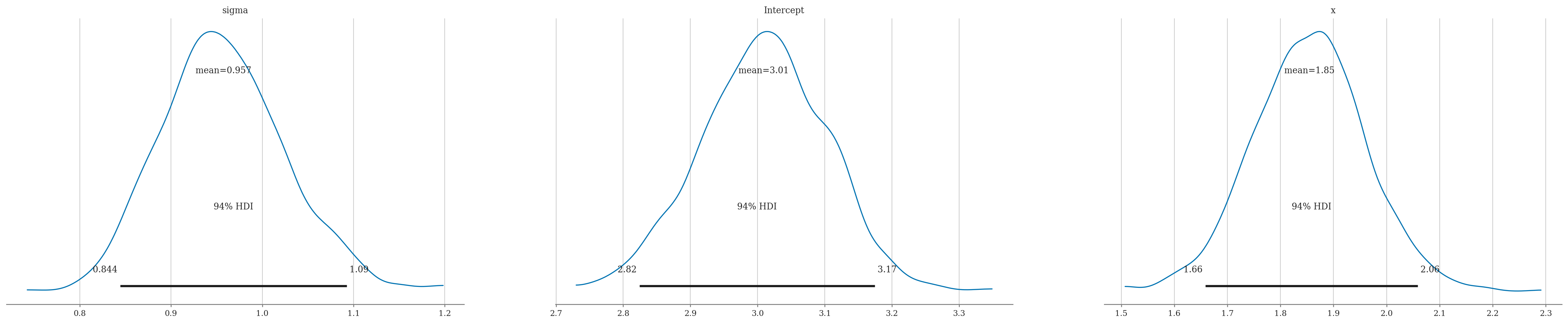
Summary using mean#

# Posterior Summary
summary = az.summary(idata, kind="stats")
summary

	mean	sd	hdi_3%	hdi_97%
sigma	0.957	0.068	0.821	1.077
Intercept	3.008	0.097	2.832	3.182
x	1.859	0.107	1.662	2.066

Summary using median as focus statistic#

ETI = Equal-Tailed Interval

az.summary(idata, stat_focus="median", kind="stats")

	median	mad	eti_3%	eti_97%
sigma	0.952	0.046	0.837	1.095
Intercept	3.008	0.067	2.836	3.192
x	1.860	0.074	1.659	2.065

# Plotting posterior
az.plot_posterior(idata, point_estimate="mean", round_to=3);

../_images/81860ddf65a038d5ebe0eb90030c5eb4906d21f46bcc57fc2ef129000051dd89.png

Investigare further

https://python.arviz.org/en/latest/api/generated/arviz.plot_lm.html

# az.plot_lm(idata)

Bonus Bayesian logistic regression example#

via file:///Users/ivan/Downloads/talks-main/pydataglobal21/index.html#15

via tomicapretto/talks

import bambi as bmb
data = bmb.load_data("ANES")
data.head()

	vote	age	party_id
0	clinton	56	democrat
1	trump	65	republican
2	clinton	80	democrat
3	trump	38	republican
4	trump	60	republican

model = bmb.Model("vote[clinton] ~ 0 + party_id + party_id:age", data, family="bernoulli")
print(model)
idata = model.fit()

Modeling the probability that vote==clinton

       Formula: vote[clinton] ~ 0 + party_id + party_id:age
        Family: bernoulli
          Link: p = logit
  Observations: 421
        Priors: 
    target = p
        Common-level effects
            party_id ~ Normal(mu: [0. 0. 0.], sigma: [1. 1. 1.])
            party_id:age ~ Normal(mu: [0. 0. 0.], sigma: [0.0586 0.0586 0.0586])

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [party_id, party_id:age]

Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 28 seconds.

We recommend running at least 4 chains for robust computation of convergence diagnostics

import pandas as pd
new_subjects = pd.DataFrame({"age": [20, 60], "party_id": ["independent"] * 2})
model.predict(idata, data=new_subjects)

# TODO: try to repdouce 
# https://github.com/tomicapretto/talks/blob/main/pydataglobal21/index.Rmd#L181-L193

One more example#

via http://www.medicine.mcgill.ca/epidemiology/joseph/courses/EPIB-682/bayesreg.pdf

Fit a logistic regression model of bone fractures with independent variables age and sex.

The true model had: \(\beta_0 = -25\), \(\beta_{\tt{sex}} = 0.5\), \(\beta_{\tt{age}} = 0.4\).

With so few data points and three parameters to estimate, do not expect posterior means/medians to equal the correct values exactly, but all would most likely be in the 95% intervals.

dfmed = pd.DataFrame(
    dict(sex=[1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1],
         age=[69, 57, 61, 60, 69, 74, 63, 68, 64, 53, 60, 58, 79, 56, 53, 74, 56, 76, 72, 56, 66, 52, 77, 70, 69, 76, 72, 53, 69, 59, 73, 77, 55, 77, 68, 62, 56, 68, 70, 60, 65, 55, 64, 75, 60, 67, 61, 69, 75, 68, 72, 71, 54, 52, 54, 50, 75, 59, 65, 60, 60, 57, 51, 51, 63, 57, 80, 52, 65, 72, 80, 73, 76, 79, 66, 51, 76, 75, 66, 75, 78, 70, 67, 51, 70, 71, 71, 74, 74, 60, 58, 55, 61, 65, 52, 68, 75, 52, 53, 70],
         frac=[1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1,
1, 0, 1, 1, 0, 0, 1, 0, 0, 1])
)
# df3

priorsmed = {
    "Intercept": bmb.Prior("Normal", mu=0, sigma=1e4),
    "sex": bmb.Prior("Normal", mu=0, sigma=1e4),
    "age": bmb.Prior("Normal", mu=0, sigma=1e4),
}

modmed = bmb.Model("frac ~ 1 + sex + age",
                 family="bernoulli",
                 link="logit",
                 priors=priorsmed,
                 data=dfmed)
modmed

       Formula: frac ~ 1 + sex + age
        Family: bernoulli
          Link: p = logit
  Observations: 100
        Priors: 
    target = p
        Common-level effects
            Intercept ~ Normal(mu: 0.0, sigma: 10000.0)
            sex ~ Normal(mu: 0.0, sigma: 10000.0)
            age ~ Normal(mu: 0.0, sigma: 10000.0)

idatamed = modmed.fit(draws=2000)
az.summary(idatamed, kind="stats")

Modeling the probability that frac==1

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [Intercept, sex, age]

Sampling 2 chains for 1_000 tune and 2_000 draw iterations (2_000 + 4_000 draws total) took 3 seconds.

We recommend running at least 4 chains for robust computation of convergence diagnostics

	mean	sd	hdi_3%	hdi_97%
Intercept	-23.797	4.642	-32.217	-15.337
sex	1.511	0.778	0.128	2.992
age	0.375	0.072	0.240	0.501

import statsmodels.formula.api as smf
lrmed = smf.logit("frac ~ 1 + sex + age", data=dfmed).fit()
lrmed.params

Optimization terminated successfully.
         Current function value: 0.297593
         Iterations 8

Intercept   -21.850408
sex           1.361099
age           0.344670
dtype: float64

Section 5.3 — Bayesian linear models

Contents

Section 5.3 — Bayesian linear models#

Notebook setup#

Bayesian model#

Example 1: students score as a function of effort#

Students dataset#

Bayesian model#

Bambi model#

Inspecting the Bambi model#

Prior predictive checks#

Model fitting and analysis#

Model predictions#

Comparing to frequentist results#

Conclusions#

Example 2: doctors sleep scores#

Doctors dataset#

Bayesian model#

Bambi model#

Prior predictive checks#

Model fitting and analysis#

Partial correlation scale?#

Comparing to frequentist results#

Conclusions#

Example 3: Bayesian logistic regression#

Interns data#

Bayesian logistic regression model#

Bambi model#

Prior predictive checks#

Model fitting and analysis#

Visualize variability of the results#

Interpretation of the parameters#

Parameters as changes in the log-odds#

Parameters as ratios of odds#

Differences in probabilities#

Predictions#

Plot predictions#

Comparing to frequentist results#

Conclusions#

Explanations#

Robust linear regression#

Shrinkage priors#

Standardizing predictors#

Discussion#

Comparison to frequentist linear models#

Causal graphs#

Next steps#

Exercises#

Exercise 1: redo some of the exercises/problems from Ch4 using Bayesian methods#

Exercise 2: redo examples of causal inference#

Exercise 3: fit model with different priors#

Exercise 4: redo logistic regression exercises from Sec 4.6#

Exercise 5: bioassay logistic regression#

Exercise 6: redo Poisson regression exercises from Sec 4.6#

Exercise 7: fit normal and robust to the dataset ??TODO?? which has outliers#

Exercise 8: PhD delays#

Links#

BONUS MATERIAL#

Simple linear regression using PyMC#

Simple linear regression on synthetic data#

Summary using mean#

Summary using median as focus statistic#

Bonus Bayesian logistic regression example#

One more example#