Section 3.6 — Statistical design and error analysis

This notebook contains the code examples from Section 3.6 Statistical design and error analysis of the No Bullshit Guide to Statistics.

Notebook setup

# load Python modules
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Plot helper functions
from ministats import plot_pdf
from ministats.utils import savefigure

# Figures setup
plt.clf()  # needed otherwise `sns.set_theme` doesn't work
from plot_helpers import RCPARAMS
RCPARAMS.update({'figure.figsize': (10, 3)})   # good for screen
# RCPARAMS.update({'figure.figsize': (5, 1.6)})  # good for print
sns.set_theme(
    context="paper",
    style="whitegrid",
    palette="colorblind",
    rc=RCPARAMS,
)

# Useful colors
snspal = sns.color_palette()
blue, orange, purple = snspal[0], snspal[1], snspal[4]

# High-resolution please
%config InlineBackend.figure_format = 'retina'

# Where to store figures
DESTDIR = "figures/stats/design"

<Figure size 640x480 with 0 Axes>

# simple float __repr__
np.set_printoptions(legacy='1.25')

# set random seed for repeatability
np.random.seed(42)

Definitions

# FIGURES ONLY
from ministats import plot_alpha_beta_errors
with sns.axes_style("ticks"), plt.rc_context({"figure.figsize":(5,1.5)}):
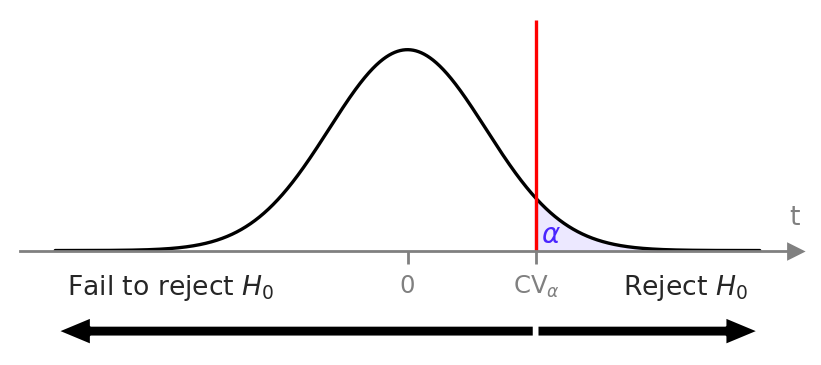
    ax = plot_alpha_beta_errors(cohend=0.1, ax=None, xlims=[-3,3], n=9,
                                show_alt=False, show_concl=True,
                                alpha_offset=(0,0.014),
                                fontsize=10)
    filename = os.path.join(DESTDIR, "H0_rejection_region.pdf")
    savefigure(ax, filename)

Design params: n = 9 , alpha = 0.05 , beta = 0.910663745890349 , Delta = 0.2 , d = 0.1 , CV = 1.0965690846343148

Saved figure to figures/stats/design/H0_rejection_region.pdf
Saved figure to figures/stats/design/H0_rejection_region.png

# FIGURES ONLY
from ministats import plot_alpha_beta_errors

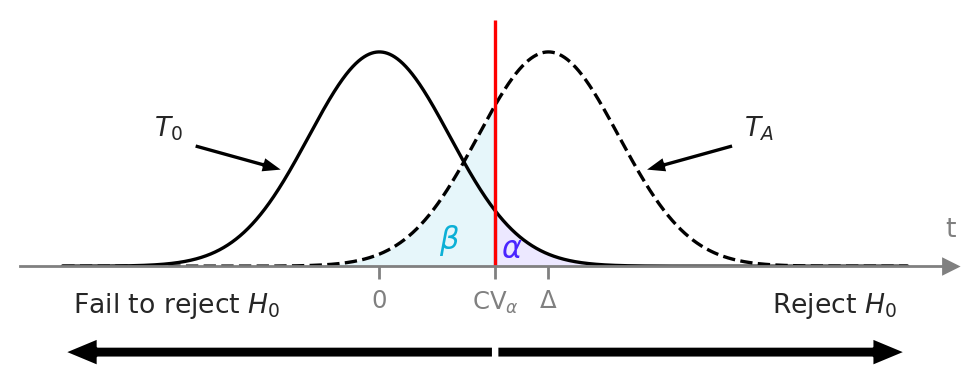
with sns.axes_style("ticks"), plt.rc_context({"figure.figsize":(6,1.6)}):
    ax = plot_alpha_beta_errors(cohend=0.8, show_dist_labels=True, show_concl=True,
                                fontsize=11,
                                alpha_offset=(0,0.013),
                                beta_offset=(-0.06,0.02))

filename = os.path.join(DESTDIR, "H0_HA_distributions_cvalue.pdf")
savefigure(ax, filename)

Design params: n = 9 , alpha = 0.05 , beta = 0.2250805806658559 , Delta = 1.6 , d = 0.8 , CV = 1.0965690846343148
Saved figure to figures/stats/design/H0_HA_distributions_cvalue.pdf

Saved figure to figures/stats/design/H0_HA_distributions_cvalue.png

Hypothesis decision rules

Decision rule based on \(p\)-values

# pre-data
alpha = ...   # chosen in advance

# post-data
obst = ...    # calculated from sample
rvT0 = ...    # sampling distribution under H0
pvalue = ...  # prob. of obst under rvT0

# make decision based on p-value
if pvalue <= alpha:
    decision = "Reject H0"
else:
    decision = "Fail to reject H0"

Simplified decision rule

# pre-data
alpha = ...     # chosen in advance
rvT0 = ...      # sampling distribution under H0
CV_alpha = ...  # calculated from alpha-quantile of rvT0

# post-data
obst = ...      # calculated from sample
# make decision based on test statistic
if obst >= CV_alpha:
    decision = "Reject H0"
else:
    decision = "Fail to reject H0"

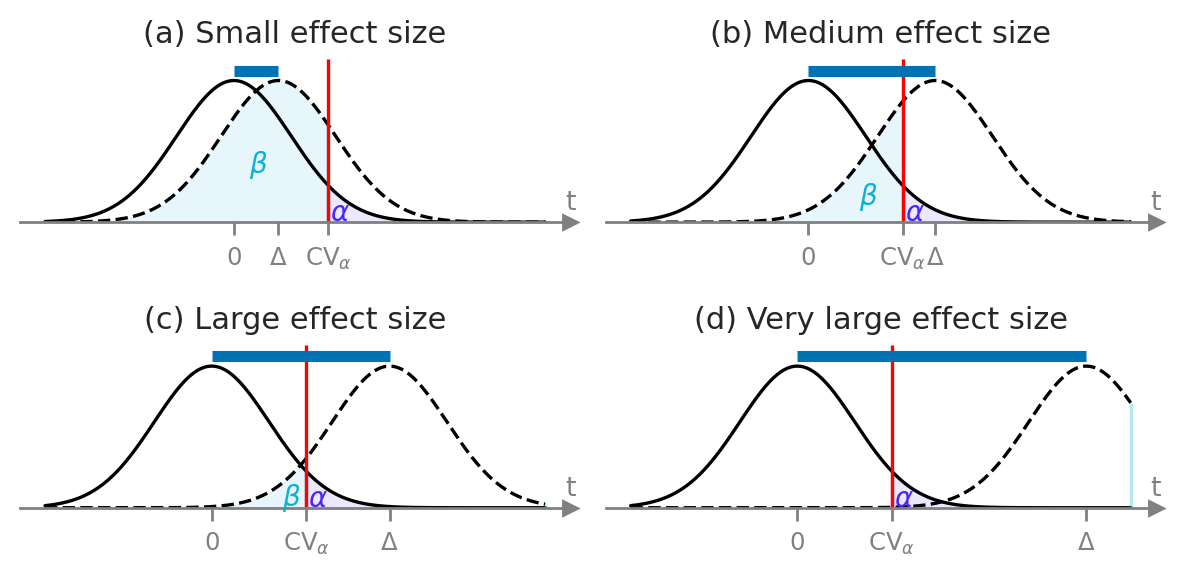
Statistical design

# FIGURES ONLY
d_small = 0.20
d_medium = 0.57 # chosen to avoid overlap between CV and Delta
d_large = 0.80
d_vlarge = 1.3

with sns.axes_style("ticks"):
    fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2,2, figsize=(6,3))
    
    plot_alpha_beta_errors(cohend=d_small,  xlims=[-1.7,2.8], n=15, ax=ax1, fontsize=10, show_es=True,
                           alpha_offset=(-0.03,0.005), beta_offset=(0.1,0.2))
    ax1.set_title("(a) Small effect size", fontsize=11)
    
    plot_alpha_beta_errors(cohend=d_medium, xlims=[-1.6,2.9], n=15, ax=ax2, fontsize=10, show_es=True,
                           alpha_offset=(-0.03,0.005), beta_offset=(0.05,0.08))
    ax2.set_title("(b) Medium effect size", fontsize=11)
    
    plot_alpha_beta_errors(cohend=d_large,  xlims=[-1.5,3], n=15, ax=ax3, fontsize=10, show_es=True,
                           alpha_offset=(-0.03,0.005), beta_offset=(0,0.02))
    ax3.set_title("(c) Large effect size", fontsize=11)
    
    plot_alpha_beta_errors(cohend=d_vlarge,  xlims=[-1.5,3], n=15, ax=ax4, fontsize=10, show_es=True,
                           alpha_offset=(-0.03,0.005), beta_offset=(-0.06,0.02))
    ax4.set_title("(d) Very large effect size", fontsize=11)

    filename = os.path.join(DESTDIR, "panel_beta_for_different_effect_sizes.pdf")
    savefigure(fig, filename)

Design params: n = 15 , alpha = 0.05 , beta = 0.8079200023112518 , Delta = 0.4 , d = 0.2 , CV = 0.8493987605509224
Design params: n = 15 , alpha = 0.05 , beta = 0.28680362819561334 , Delta = 1.14 , d = 0.57 , CV = 0.8493987605509224
Design params: n = 15 , alpha = 0.05 , beta = 0.07303790512845224 , Delta = 1.6 , d = 0.8 , CV = 0.8493987605509224

Design params: n = 15 , alpha = 0.05 , beta = 0.0003494316033385532 , Delta = 2.6 , d = 1.3 , CV = 0.8493987605509224

Saved figure to figures/stats/design/panel_beta_for_different_effect_sizes.pdf
Saved figure to figures/stats/design/panel_beta_for_different_effect_sizes.png

# FIGURES ONLY
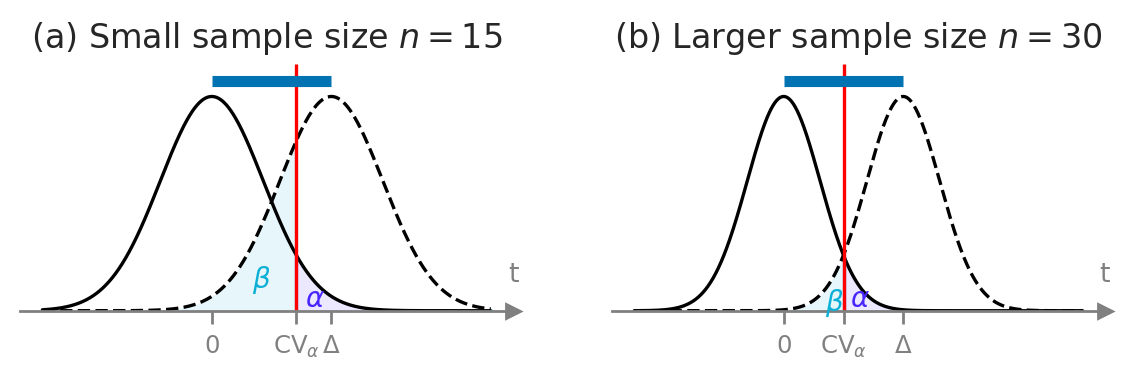
Delta = 0.6

# TODO: check this figure --> results for n=15 seem to be too good to be true...
with sns.axes_style("ticks"):
    fig, (ax1, ax2) = plt.subplots(1,2, figsize=(7,1.6))
    
    n1 = 15
    plot_alpha_beta_errors(cohend=Delta,  xlims=[-1.7,2.8], n=n1, ax=ax1, fontsize=10, show_es=True,
                           alpha_offset=(0.03,0.005), beta_offset=(0,0.05))
    ax1.set_title(f"(a) Small sample size $n={n1}$", fontsize=12)
    
    n2 = 30
    plot_alpha_beta_errors(cohend=Delta,  xlims=[-1.5,3], n=n2, ax=ax2, fontsize=10, show_es=True,
                           alpha_offset=(0.005,0), beta_offset=(0.04,0.01))
    ax2.set_title(f"(b) Larger sample size $n={n2}$", fontsize=12)

    filename = os.path.join(DESTDIR, "panel_beta_for_different_sample_sizes.pdf")
    savefigure(fig, filename)

Design params: n = 15 , alpha = 0.05 , beta = 0.24858908649659617 , Delta = 1.2 , d = 0.6 , CV = 0.8493987605509224
Design params: n = 30 , alpha = 0.05 , beta = 0.0503487295055579 , Delta = 1.2 , d = 0.6 , CV = 0.6006156235170058

Saved figure to figures/stats/design/panel_beta_for_different_sample_sizes.pdf
Saved figure to figures/stats/design/panel_beta_for_different_sample_sizes.png

# FIGURES ONLY
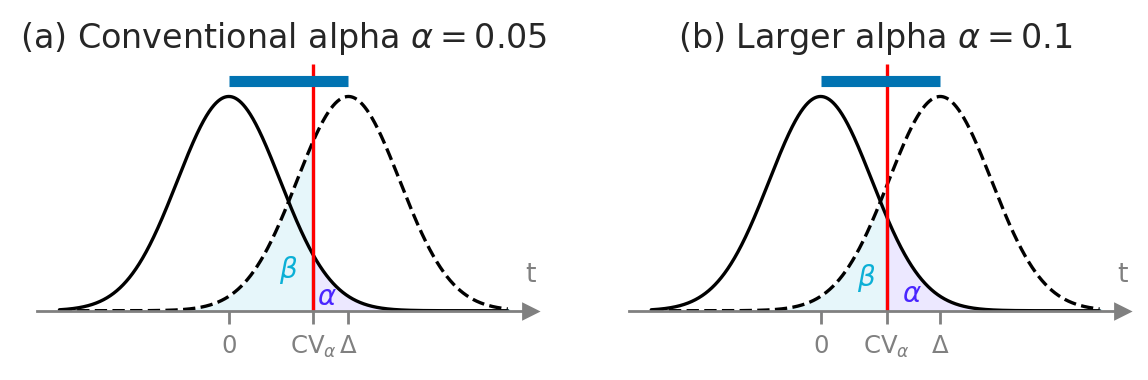
Delta = 0.6

with sns.axes_style("ticks"):
    fig, (ax1, ax2) = plt.subplots(1,2, figsize=(7,1.6))
    
    n1 = 15
    alpha1 = 0.05
    plot_alpha_beta_errors(alpha=alpha1, cohend=Delta, xlims=[-1.7,2.8], n=15, ax=ax1, fontsize=10, show_es=True,
                           alpha_offset=(-0.02,0.005), beta_offset=(0.1,0.1))
    ax1.set_title(r"(a) Conventional alpha $\alpha=0.05$", fontsize=12)

    alpha2 = 0.1
    plot_alpha_beta_errors(alpha=alpha2, cohend=Delta, xlims=[-1.7,2.8], n=15, ax=ax2, fontsize=10, show_es=True,
                           alpha_offset=(0,0.005), beta_offset=(0.05,0.05))
    ax2.set_title(r"(b) Larger alpha $\alpha=0.1$", fontsize=12)

    filename = os.path.join(DESTDIR, "panel_beta_for_different_alphas.pdf")
    savefigure(fig, filename)

Design params: n = 15 , alpha = 0.05 , beta = 0.24858908649659617 , Delta = 1.2 , d = 0.6 , CV = 0.8493987605509224
Design params: n = 15 , alpha = 0.1 , beta = 0.14865057213685162 , Delta = 1.2 , d = 0.6 , CV = 0.6617903827547039

Saved figure to figures/stats/design/panel_beta_for_different_alphas.pdf
Saved figure to figures/stats/design/panel_beta_for_different_alphas.png

Cohen’s d standardized effect size

The effect size \(\Delta\) we use in statistical design is usually expressed as a standardized effect size like Cohen’s \(d\), which is defined as the observed “difference” divided by a standard deviation of the theoretical model under the null hypothesis.

One-sample case

For a one-sample test of the mean relative to a null model with mean \(\mu_0\), Cohen’s \(d\) is calculated as:

\[ d = \frac{\overline{\mathbf{x}} - \mu_0}{ s_{\mathbf{x}} }, \]

where \(s_{\mathbf{x}}\) is the sample standard deviation.

When doing statistical design, we haven’t obtained the sample \(\mathbf{x}\) yet so we don’t know what its standard deviation \(s_{\mathbf{x}}\) will be, so we have to make an educated guess of this value, which usually means using the standard deviation of the theoretical model \(\sigma_{X_0}\).

Two-sample case

For a two-sample test for the difference between means, Cohen’s \(d\) is defined as the difference between sample means divided by the pooled standard deviation:

\[ d = \frac{\overline{\mathbf{x}} - \overline{\mathbf{y}} }{ s_{p} }. \]

where the formula for the pooled variance is \(s_{p}^2 = [(n -1)s_{\mathbf{x}}^2 + (m -1)s_{\mathbf{y}}^2]/(n + m -2)\).

When doing statistical design, we don’t know the standard deviations \(s_{\mathbf{x}}\) and \(s_{\mathbf{y}}\) so we replace them with the theoretical standard deviations \(\sigma_{X_0}\) and \(\sigma_{Y_0}\) under the null hypothesis.

Recall table of reference values for Cohen’s \(d\) standardized effect sizes, suggested by Cohen in (Cohen YYYY TODO).

Cohen’s d	Effect size
0.01	very small
0.20	small
0.50	medium
0.80	large

The formulas for sample size planning and power calculations we’ll present below are based on Cohen’s \(d\).

This means you’ll have to express your guess about the effect size \(\Delta\) as \(d = \frac{\Delta}{\sigma_0}\) where \(\sigma_0\) is your best about the standard deviation of the theoretical distribution.

Note Cohen’s \(d\) is based on the standard deviations of the “raw” theoretical population, and not standard error.

Example 1: detect kombuncha volume deviation from theory

Design Type A: choose \(\alpha=0.05\), \(\beta=0.2\), \(\Delta_{\textrm{min}} = 4\;\text{ml}\) then calculate required sample size \(n\). We’ll assume \(\sigma=10\).

alpha = 0.05
beta = 0.2
Delta_min = 4

# assumption
sigma = 10

from scipy.stats import norm
rvZ = norm(loc=0, scale=1)

z_u = rvZ.ppf(1-alpha)
z_l = rvZ.ppf(beta)

n_approx = (z_u - z_l)**2 * sigma**2 / Delta_min**2
n_approx

38.64098270012354

Using statsmodels

To use the statsmodels sample size estimation function, we’ll need to express the effect size \(\Delta=4\) in terms of Cohen’s \(d\).

d = Delta_min / sigma
d

0.4

from statsmodels.stats.power import TTestPower
ttp = TTestPower()
n = ttp.solve_power(effect_size=d, alpha=0.05, power=0.8,
                    alternative="larger")
n

40.02907613995643

from scipy.stats import t as tdist

rvT0 = tdist(df=n-1)
CV_alpha = rvT0.ppf(0.95)
CV_alpha

1.6848445860460983

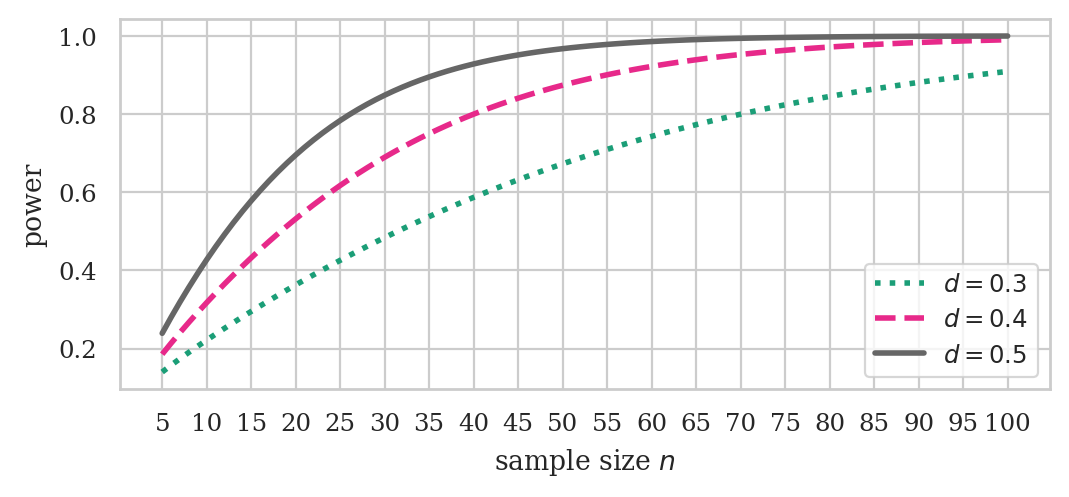
ds = np.array([0.3, 0.4, 0.5])
ns = np.arange(5, 101)
fig, ax = plt.subplots(figsize=(6,2.4))
ttp.plot_power(dep_var="nobs", ax=ax,
               effect_size=ds, nobs=ns, alpha=0.05,
               alternative="larger")
ax.set_xticks( np.arange(5,105,5) )
# ax.set_title("Power of t-test vs. sample size for different effect sizes")
ax.set_title(None)
ax.set_xlabel("sample size $n$")
ax.set_ylabel("power")
# set custom line styles
linestyles = ["dotted", "dashed", "solid"]
for line, ls in zip(ax.get_lines(), linestyles):
    line.set_linestyle(ls)
# set custom legend
labels = [f"$d={d}$" for d in ds]
ax.legend(ax.get_lines(), labels, loc="lower right")

# FIGURES ONLY
filename = os.path.join(DESTDIR, "plot_one_sample_t_power_vs_sample_size.pdf")
savefigure(fig, filename)

Saved figure to figures/stats/design/plot_one_sample_t_power_vs_sample_size.pdf
Saved figure to figures/stats/design/plot_one_sample_t_power_vs_sample_size.png

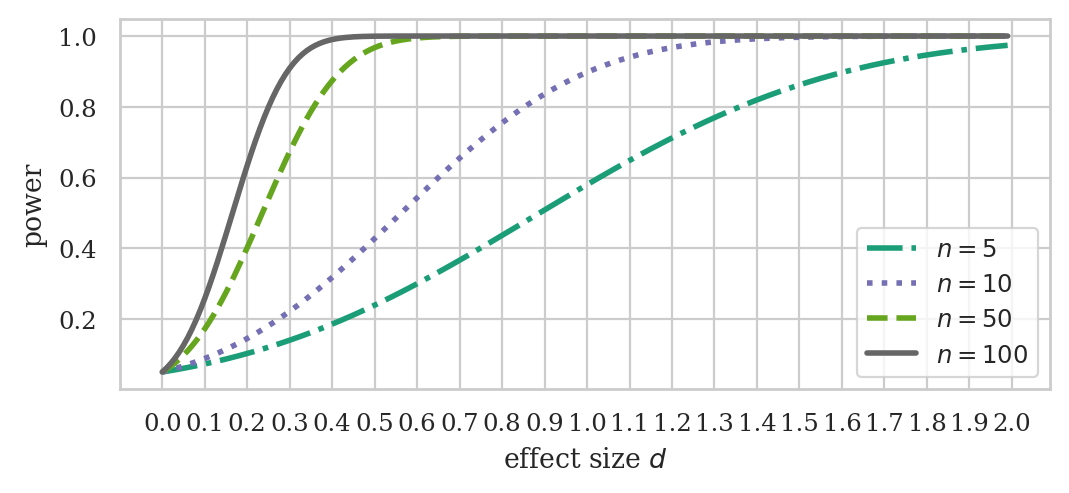
ds = np.arange(0, 2, 0.01)
ns = np.array([5, 10, 50, 100])
fig, ax = plt.subplots(figsize=(6,2.4))
ttp.plot_power(dep_var="effect size", ax=ax,
               effect_size=ds, nobs=ns, alpha=0.05,
               alternative="larger")
ax.set_xticks( np.arange(0, 2+0.1, 0.1) )
# ax.set_title("Power of t-test vs. effect size for different sample sizes")
ax.set_title(None)
ax.set_xlabel("effect size $d$")
ax.set_ylabel("power")

# set custom line styles
linestyles = ["dashdot", "dotted", "dashed", "solid"]
for line, ls in zip(ax.get_lines(), linestyles):
    line.set_linestyle(ls)
# set custom legend
labels = [f"$n={n}$" for n in ns]
ax.legend(ax.get_lines(), labels)

# FIGURES ONLY
filename = os.path.join(DESTDIR, "plot_one_sample_t_power_vs_effect_size.pdf")
savefigure(fig, filename)

Saved figure to figures/stats/design/plot_one_sample_t_power_vs_effect_size.pdf
Saved figure to figures/stats/design/plot_one_sample_t_power_vs_effect_size.png

Data collection

kombuchapop = pd.read_csv("../datasets/kombuchapop.csv")
batch55pop = kombuchapop[kombuchapop["batch"]==55]
kpop55 = batch55pop["volume"]

We can select a random sample of size \(n=41\) from the populaiton kpop55 by calling the .sample method.

np.random.seed(52)
n = 41  # rounding up
ksample55 = kpop55.sample(n)
len(ksample55)

41

# Uncomment to see the observed sample
# ksample55.values

# Observed sample mean
np.mean(ksample55)

1002.300975609756

# Observed effect size from Batch 55
Delta_hat = np.mean(ksample55) - 1000
Delta_hat

2.300975609756051

Statistical analysis on the sample from Batch 55

CV_alpha  # = tdist(df=n-1).ppf(0.95)

1.6848445860460983

kbar55 = ksample55.mean()
sehat55 =  ksample55.std() / np.sqrt(n)

t55 = (kbar55 - 1000) / sehat55
t55

1.643970432409751

We can now apply the simplified decision rule that compares the test statistic t55 to the cutoff value CV_alpha.

if t55 >= CV_alpha:
    decision = "Reject H0"
else:
    decision = "Fail to reject H0"
decision

'Fail to reject H0'

Alternatively, we can make the decision whether to reject \(H_0\) or not using the “old” decision rule that compares the \(p\)-value to the cutoff \(\alpha=0.05\). We can compute the p-value from ttest_mean function we defined in Section 3.4, see 34_analytical_approx.ipynb.

from ministats import ttest_mean
pvalue55 = ttest_mean(ksample55, mu0=1000)
if pvalue55 <= 0.05:
    decision = "Reject H0"
else:
    decision = "Fail to reject H0"
decision

'Fail to reject H0'

# # ALT2. Use the p-value form a direct simulation test
# from ministats import simulation_test_mean
# simulation_test_mean(ksample55, mu0=1000, sigma0=10)

Example 2: comparison of East vs. West electricity prices

eprices = pd.read_csv("../datasets/eprices.csv")
eprices.groupby("loc").describe()

	price
	count	mean	std	min	25%	50%	75%	max
loc
East	9.0	6.155556	0.877655	4.8	5.5	6.3	6.5	7.7
West	9.0	9.155556	1.562139	6.8	8.3	8.6	10.0	11.8

Need a guess the effect size, which we’ll express in terms of Cohen’s \(d\). We choose \(d=1\), which corresponds to a difference of one cent \(\Delta_{\text{min}} = 1\), assuming the standard deviation of the prices is around \(\sigma=1\).

cohend2_min = 1

Solving for a desired power

The function solve_power takes as argument the chosen level of power, and two of the three other design parameters alpha, nobs1, and effect_size, and calculates the value of the third parameter required to achieve the chosen level of power \(=(1-\beta)\).

from statsmodels.stats.power import TTestIndPower
ttindp = TTestIndPower()

# power of two-sample t-test assuming cohend2_min and n=m=9 
ttindp.power(effect_size=cohend2_min, nobs1=9, 
             alpha=0.05, alternative="two-sided")

0.5133625331068465

The Type II error rate \(\beta\) of this test is

1 - 0.5133625331068463

0.4866374668931537

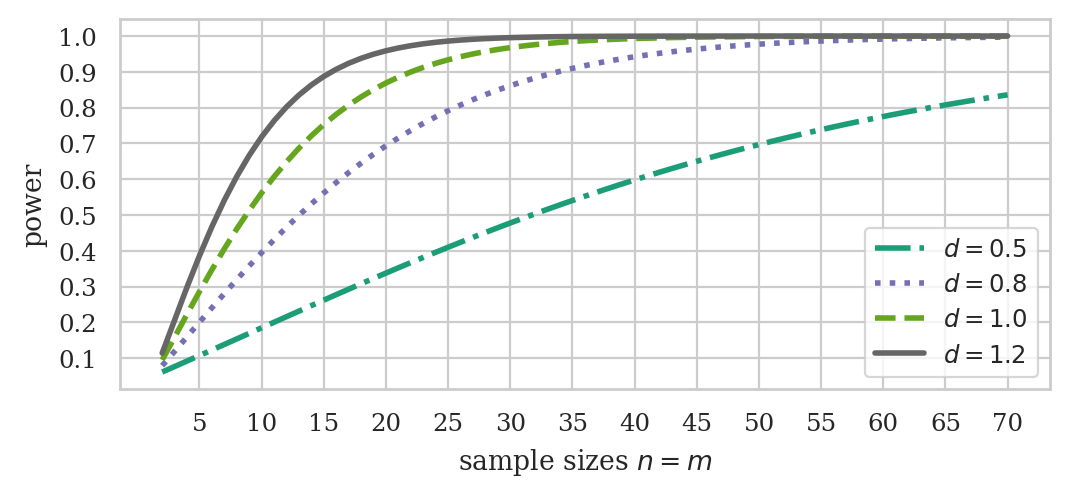
ds = np.array([0.5, 0.8, 1.0, 1.2])
ns = np.arange(2, 71)
fig, ax = plt.subplots(figsize=(6,2.4))
ttindp.plot_power(dep_var="nobs", ax=ax,
                  effect_size=ds, nobs=ns, alpha=0.05,
                  alternative="two-sided")
ax.set_xticks( np.arange(5,75,5) )
# ax.set_title("Power of two-sample t-test vs. sample size $n=m$ for different effect sizes")
ax.set_title(None)
ax.set_xlabel("sample sizes $n=m$")
ax.set_yticks([0.1, 0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0])
ax.set_ylabel("power")

# set custom line styles
linestyles = ["dashdot", "dotted", "dashed", "solid"]
for line, ls in zip(ax.get_lines(), linestyles):
    line.set_linestyle(ls)
# set custom legend
labels = [f"$d={d}$" for d in ds]
ax.legend(ax.get_lines(), labels)

filename = os.path.join(DESTDIR, "plot_two_sample_t_power_vs_sample_size.pdf")
savefigure(fig, filename)

Saved figure to figures/stats/design/plot_two_sample_t_power_vs_sample_size.pdf
Saved figure to figures/stats/design/plot_two_sample_t_power_vs_sample_size.png

If Bob wants to achieve 80% power for future price comparison tests, he needs to collect samples of size \(n=1\) or larger.

ttindp.solve_power(effect_size=cohend2_min, power=0.8, alpha=0.05,
                   alternative="two-sided")

16.71472244695402

Calculate minimum effect size

# minimum effect size to achieve 80% power when n=m=9
ttindp.solve_power(alpha=0.05, power=0.8, nobs1=9,
                   alternative="two-sided")

1.406924652680254

(optional) Calculate sample size needed to achieve 0.8 power

# minimum sample size required to achieve 80% power when effect size is d=1
ttindp.solve_power(effect_size=1.0, alpha=0.05, power=0.8,
                   alternative="two-sided")

16.71472244695402

Alternative calculation methods

Using G*Power

TODO: add sceenshots

Using pingouin

import pingouin as pg

Sample size for the one-sample \(t\)-test

pg.power_ttest(alpha=0.05, power=0.8, d=0.4,
               contrast="one-sample", alternative="greater")

40.029076225855356

We can also verify that \(n=41\) produces a test with \(80\%\) power.

pg.power_ttest(alpha=0.05, n=41, d=0.4,
               contrast="one-sample", alternative="greater")

0.8085822361693652

Power of Bob’s two-sample \(t\)-test

# power of two-sample t-test assuming d=1 and n=m=9 
pg.power_ttest(alpha=0.05, n=9, d=1,
               contrast="two-samples", alternative="two-sided")

0.5133625331068465

Explanations

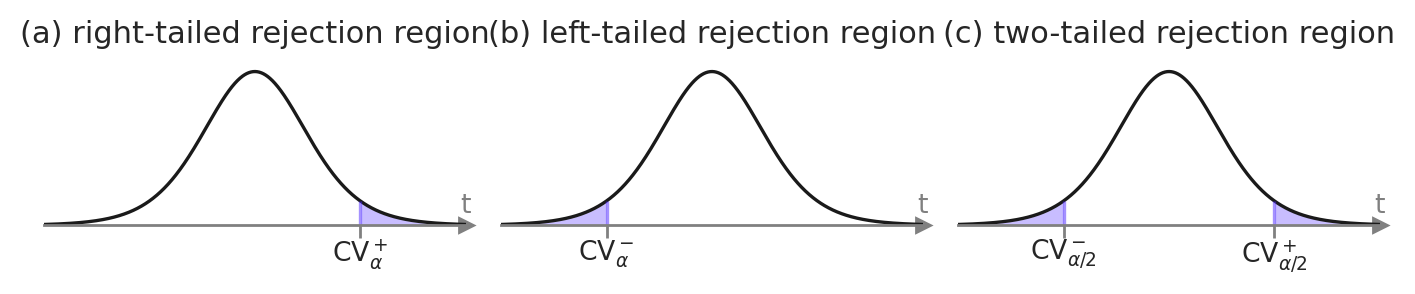
One-sided and two-sided rejection regions

from scipy.stats import t as tdist
rvT0 = tdist(df=9)

alpha = 0.05

# right-tailed rejection region
rvT0.ppf(alpha)

-1.8331129326536337

# left-tailed rejection region
rvT0.ppf(1-alpha)

1.8331129326536335

# two-sided rejection region
rvT0.ppf(alpha/2), rvT0.ppf(1 - alpha/2)

(-2.2621571628540997, 2.2621571628540993)

filename = os.path.join(DESTDIR, "panel_rejection_regions_left_twotailed_right.pdf")
    
from scipy.stats import t as tdist
rvT = tdist(df=9)

xs = np.linspace(-4, 4, 1000)
ys = rvT.pdf(xs)

# design choices
transp = 0.3
alpha_color = "#4A25FF"
beta_color = "#0CB0D6"
axis_color = "#808080"

def plot_rejection_region(ax, xs, ys, alt, title):
    ax.set_title(title, fontsize=11)

    # manually add arrowhead to x-axis + label t at the end
    ax.plot(1, 0, ">", color=axis_color, transform=ax.get_yaxis_transform(), clip_on=False)
    ax.set_xlabel("t")
    ax.xaxis.set_label_coords(1, 0.2)

    sns.lineplot(x=xs, y=ys, ax=ax, color="k")
    ax.set_xlim(-4, 4)
    ax.set_ylim(0, 0.42)
    ax.set_xticklabels([])
    ax.set_yticks([])
    ax.spines[['left', 'right', 'top']].set_visible(False)
    ax.spines['bottom'].set_color(axis_color)
    ax.tick_params(axis='x', colors=axis_color)
    ax.xaxis.label.set_color(axis_color)
    
    if alt == "greater":
        ax.set_xticks([2])
        # highlight the right tail
        mask = (xs > 2)
        ax.fill_between(xs[mask], y1=ys[mask], alpha=transp, facecolor=alpha_color)
        ax.vlines([2], ymin=0, ymax=rvT.pdf(2), linestyle="-", alpha=transp+0.2, color=alpha_color)
        ax.text(2, -0.03, r"$\mathrm{CV}_{\alpha}^+$", verticalalignment="top", horizontalalignment="center")

    elif alt == "less":
        ax.set_xticks([-2])
        # highlight the left tail
        mask = (xs < -2)
        ax.fill_between(xs[mask], y1=ys[mask], alpha=transp, facecolor=alpha_color)
        ax.vlines([-2], ymin=0, ymax=rvT.pdf(-2), linestyle="-", alpha=transp+0.2, color=alpha_color)
        ax.text(-2, -0.03, r"$\mathrm{CV}_{\alpha}^-$", verticalalignment="top", horizontalalignment="center")

    elif alt == "two-sided":
        ax.set_xticks([-2,2])
        # highlight the left and right tails
        mask = (xs < -2)
        ax.fill_between(xs[mask], y1=ys[mask], alpha=transp, facecolor=alpha_color)
        ax.vlines([-2], ymin=0, ymax=rvT.pdf(-2), linestyle="-", alpha=transp+0.2, color=alpha_color)
        ax.text(-2, -0.03, r"$\mathrm{CV}_{\alpha/2}^-$", verticalalignment="top", horizontalalignment="center")
        mask = (xs > 2)
        ax.fill_between(xs[mask], y1=ys[mask], alpha=transp, facecolor=alpha_color)
        ax.vlines([2], ymin=0, ymax=rvT.pdf(2), linestyle="-", alpha=transp+0.2, color=alpha_color)
        ax.text(2, -0.03, r"$\mathrm{CV}_{\alpha/2}^+$", verticalalignment="top", horizontalalignment="center")


with sns.axes_style("ticks"), plt.rc_context({"figure.figsize":(7,1.6)}):
    fig, (ax3, ax1, ax2) = plt.subplots(1,3)

    # RIGHT
    title = '(a) right-tailed rejection region'
    plot_rejection_region(ax3, xs, ys, "greater", title)

    # LEFT
    title = '(b) left-tailed rejection region'
    plot_rejection_region(ax1, xs, ys, "less", title)

    # TWO-TAILED
    title = '(c) two-tailed rejection region'
    plot_rejection_region(ax2, xs, ys, "two-sided", title)

savefigure(fig, filename)

Saved figure to figures/stats/design/panel_rejection_regions_left_twotailed_right.pdf
Saved figure to figures/stats/design/panel_rejection_regions_left_twotailed_right.png

Derivation of the sample size planning formula

MAYBE show math steps

Discussion

A conceptual amalgam of two ideas

Steps of the Neyman—Pearson hypothesis test

1. Calculate the cutoff value \(\text{CV}_{\alpha}\).

2. Calculate the test statistic \(t_{55}\) from the sample \(\mathbf{k}_{55}\).

3. Apply the simplified decision rule that compares the test statistic to the cutoff value.

# 1. Calculate the critical value
from scipy.stats import t as tdist
rvT0 = tdist(df=n-1)
CV_alpha = rvT0.ppf(0.95)
CV_alpha

1.6838510133356523

# 2. Calculate the test statistic
n = len(ksample55)
kbar55 = ksample55.mean()
sehat55 =  ksample55.std() / np.sqrt(n)
t55 = (kbar55 - 1000) / sehat55
t55

1.643970432409751

# 3. Compare the test-statistic to the critical value
if t55 >= CV_alpha:
    decision = "Reject H0"
else:
    decision = "Fail to reject H0"
decision

'Fail to reject H0'

Steps of the Fisherian hypothesis test

1. Calculate the test statistic \(t_{55}\).

2. Calculate the \(p\)-value of the statistic from the sampling distribution under \(H_0\).

3. Make a decision whether to reject \(H_0\) by comparing the \(p\)-value to the cutoff \(\alpha=0.05\).

# 1. Calculate the test statistic
n = len(ksample55)
kbar55 = ksample55.mean()
sehat55 =  ksample55.std() / np.sqrt(n)
t55 = (kbar55 - 1000) / sehat55
t55

1.643970432409751

# 2. Calculate the $p$-value
from scipy.stats import t as tdist
rvT0 = tdist(df=n-1)
pvalue55 = 1 - rvT0.cdf(t55)   # right-tailed p-value
pvalue55

0.054010269315395765

By the way, we can also obtain the \(p\)-value by calling the helper function ttest_mean that we defined in Section 3.4, see 34_analytical_approx.ipynb.

from ministats import ttest_mean
ttest_mean(ksample55, mu0=1000, alt="greater")

0.054010269315395765

# 3. Compare the p-value to the cutoff alpha
if pvalue55 <= 0.05:
    decision = "Reject H0"
else:
    decision = "Fail to reject H0"
decision

'Fail to reject H0'

We see the results of the Neyman–Pearson and Fisherian decision rules are the same. Indeed, we’ll always come to the same decision, whether we use criterion \(p < \alpha\) in the space of \(p\)-values, or the \(t_{55} \geq \text{CV}_{\alpha}\) in the space of \(t\)-values.

Post-hoc power analysis

# Observed effect size from Batch 55
Delta_hat = np.mean(ksample55) - 1000
Delta_hat

2.300975609756051

# Observed effect size as Cohen's d
d_hat = Delta_hat / 10
d_hat

0.23009756097560513

The post-hoc power for the test we performed in Example~1 is:

from statsmodels.stats.power import TTestPower
ttp = TTestPower()
ttp.power(alpha=0.05, nobs=41, effect_size=d_hat, alternative="larger")

0.4221204906778596

It’s not clear what this power means…

Unique value proposition of hypothesis testing

Exercises

Exercise {exercise:sensitivity-of-one-sample-t-test-n-10}

from statsmodels.stats.power import TTestPower
ttp = TTestPower()
ttp.solve_power(alpha=0.05, power=0.8, nobs=10, alternative="larger")

0.8528391375721194

Exercise {exercise:power-of-two-sample-t-test-n-17}

from statsmodels.stats.power import TTestIndPower
ttindp = TTestIndPower()
ttindp.power(alpha=0.05, nobs1=17, effect_size=1, alternative="two-sided")

0.80703671514722

Links