One-sample t-test for the mean#
The goal of the one-sample \(t\)-test to check if the mean \(\mu\) of an unknown population \(X \sim \mathcal{N}(\mu, \sigma_0)\), equals the mean \(\mu_0\) of a theoretical distribution \(X_0 \sim \mathcal{N}(\mu_0, \sigma_0)\). We’ll estimate the standard deviation \(\sigma_0\) from the sample standard deviation \(\mathbf{s}_{\mathbf{x}}\). We discussed this hypothesis test in notebooks/34_analytical_approx.ipynb.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
\(\def\stderr#1{\mathbf{se}_{#1}}\) \(\def\stderrhat#1{\hat{\mathbf{se}}_{#1}}\) \(\newcommand{\Mean}{\textbf{Mean}}\) \(\newcommand{\Var}{\textbf{Var}}\) \(\newcommand{\Std}{\textbf{Std}}\) \(\newcommand{\Freq}{\textbf{Freq}}\) \(\newcommand{\RelFreq}{\textbf{RelFreq}}\) \(\newcommand{\DMeans}{\textbf{DMeans}}\) \(\newcommand{\Prop}{\textbf{Prop}}\) \(\newcommand{\DProps}{\textbf{DProps}}\)
Data#
One sample of numerical observations \(\mathbf{x}=[x_1, x_2, \ldots, x_n]\).
Modeling assumptions#
We model the unknown population as…
and the theoretical distribution is…
We assume the population is normally distributed \(\textbf{(NORM)}\), or the sample is large enough \(\textbf{(LARGEn)}\).
We also assume that the variance of the unknown population is known and equal to the variance of the theoretical population under \(H_0\)
Hypotheses#
\(H_0: \mu = \mu_0\) and \(H_A: \mu \neq \mu_0\), where \(\mu\) is the unknown population mean, \(\mu_0\) is the theoretical mean we are comparing to.
Statistical design#
for \(n=5\) …
for \(n=20\) …
Estimates#
Calculate the sample mean \(\overline{\mathbf{x}} = \Mean(\mathbf{x})\) and the sample standard deviation \(s_{\mathbf{x}} = \Std(\mathbf{x})\). We can then calculate the estimated standard error of the mean \(\stderrhat{\overline{\mathbf{x}}} = \frac{ s_{\mathbf{x}} }{ \sqrt{n} }\).
Test statistic#
Compute \(t = \frac{\overline{\mathbf{x}} - \mu_0}{ \stderrhat{\overline{\mathbf{x}}} }\) from the sample mean \(\overline{\mathbf{x}}\), the theoretical population mean \(\mu_0\), the estimated standard error \(\stderrhat{\overline{\mathbf{x}}}\).
Sampling distribution#
Student’s \(t\)-distribution with \(\nu=n-1\) degrees of freedom.
P-value calculation#
from ministats import ttest_mean
%psource ttest_mean
To perform the one-sample \(t\)-test on the sample xs,
we call ttest_mean(xs, mu0=...),
with ... replaced by the expected mean \(\mu_{X_0}\) of the theoretical population under \(H_0\)
Examples#
For all the examples we present below, we assume the theoretical distribution we expect under the null hypothesis, is normally distributed with mean \(\mu_{X_0}=100\) and standard deviation \(\sigma_{X_0} = 5\):
from scipy.stats import norm
muX0 = 100
sigmaX0 = 5
rvX0 = norm(muX0, sigmaX0)
Example A: population different from \(H_0\)#
Suppose the unknown population is normally distributed with mean \(\mu_{X_A}=104\) and standard deviation \(\sigma_{X_A} = 3\):
muXA = 104
sigmaXA = 3
rvXA = norm(muXA, sigmaXA)
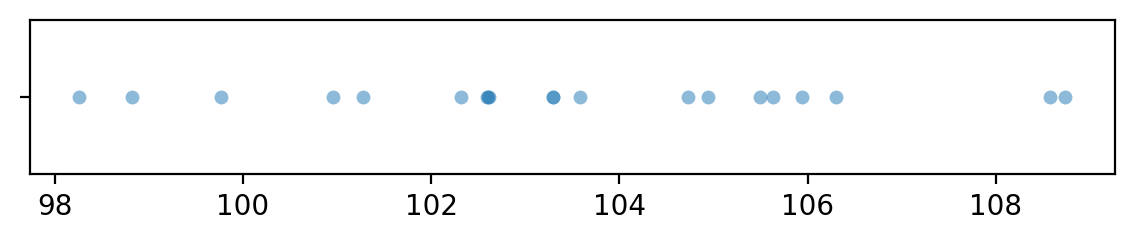
Let’s generate a sample xAs of size \(n=20\) from the random variable \(X = \texttt{rvXA}\).
np.random.seed(42)
# generate a random sample of size n=20
n = 20
xAs = rvXA.rvs(n)
xAs
array([105.49014246, 103.5852071 , 105.94306561, 108.56908957,
103.29753988, 103.29758913, 108.73763845, 106.30230419,
102.59157684, 105.62768013, 102.60974692, 102.60281074,
104.72588681, 98.26015927, 98.8252465 , 102.31313741,
100.96150664, 104.942742 , 101.27592777, 99.7630889 ])
import seaborn as sns
with plt.rc_context({"figure.figsize":(7,1)}):
sns.stripplot(x=xAs, jitter=0, alpha=0.5)
To obtain the \(p\)-value, we first compute the observed \(t\)-statistic, then calculate the tail probabilities in the two tails of the standard normal distribution \(T_0 \sim \mathcal{T}(\nu)\).
from scipy.stats import t as tdist
obsmean = np.mean(xAs)
std = np.std(xAs, ddof=1)
sehat = std / np.sqrt(n)
obst = (obsmean - muX0) / sehat
rvT0 = tdist(df=n-1)
pvalue = rvT0.cdf(-obst) + 1-rvT0.cdf(obst)
obst, pvalue
(np.float64(5.413149619618617), np.float64(3.186228235607658e-05))
The helper function ttest_mean from the ministats module performs
exactly the same sequence of steps to compute the \(p\)-value.
from ministats import ttest_mean
ttest_mean(xAs, mu0=muX0)
np.float64(3.1862282356088544e-05)
The \(p\)-value we obtain is 0.00003186,
which is below the cutoff value \(\alpha=0.05\),
so our conclusion is we reject the null hypothesis:
the mean of the sample xAs is not statistically significantly different from the theoretically expected mean \(\mu_{X_0} = 100\).
Example B: sample from a population as expected under \(H_0\)#
# unknown population X = X0
rvXB = norm(muX0, sigmaX0)
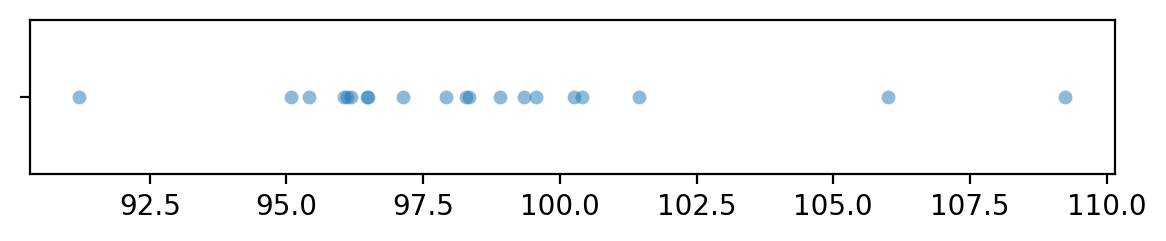
Let’s generate a sample xBs of size \(n=20\) from the random variable \(X = \texttt{rvX}\),
which has the same distribution as the theoretical distribution we expect under the null hypothesis.
# np.random.seed(32) produces false positie
np.random.seed(31)
# generate a random sample of size n=20
n = 20
xBs = rvXB.rvs(n)
xBs
array([ 97.92621393, 98.33315666, 100.40545993, 96.04486524,
98.90700164, 96.18401578, 96.11439878, 109.24678261,
96.47199845, 99.56978983, 101.43966651, 99.34306739,
95.08627924, 95.40604357, 105.99717245, 98.29312879,
91.20696344, 100.25558735, 97.14035504, 96.49716979])
import seaborn as sns
with plt.rc_context({"figure.figsize":(7,1)}):
sns.stripplot(x=xBs, jitter=0, alpha=0.5)
from ministats import ttest_mean
ttest_mean(xBs, mu0=muX0)
np.float64(0.1013574486082352)
The \(p\)-value we obtain is 0.10, which is above the cutoff value \(\alpha=0.05\)
so our conclusion is that we’ve failed to reject the null hypothesis:
the mean of the sample xBs is not significantly different from the theoretically expected mean \(\mu_{X_0} = 100\).
Confidence interval for the unknown mean#
from ministats import ci_mean
The confidence interval for the unknown population mean \(\mu_A\) in Example A is:
ci_mean(xAs, alpha=0.1, method='a')
[np.float64(102.3725312980782), np.float64(104.59967733327082)]
ci_mean(xBs, alpha=0.1, method='a')
[np.float64(96.98044495642183), np.float64(100.00646668579604)]