Section 2.6 — Inventory of continuous distributions#
This notebook contains all the code examples from Section 2.6 Inventory of continuous distributions of the No Bullshit Guide to Statistics.
Notebook setup#
# load Python modules
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Figures setup
sns.set_theme(
context="paper",
style="whitegrid",
palette="colorblind",
rc={'figure.figsize': (6,2)},
)
%config InlineBackend.figure_format = 'retina'
# set random seed for repeatability
np.random.seed(42)
%pip install --quiet ministats
Note: you may need to restart the kernel to use updated packages.
from ministats import plot_pdf
from ministats import plot_cdf
from ministats import plot_pdf_and_cdf
Uniform distribution#
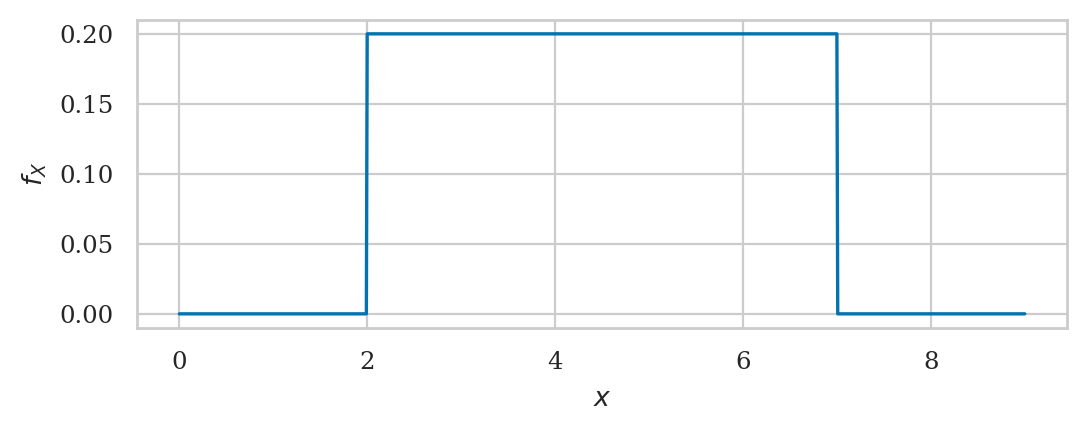
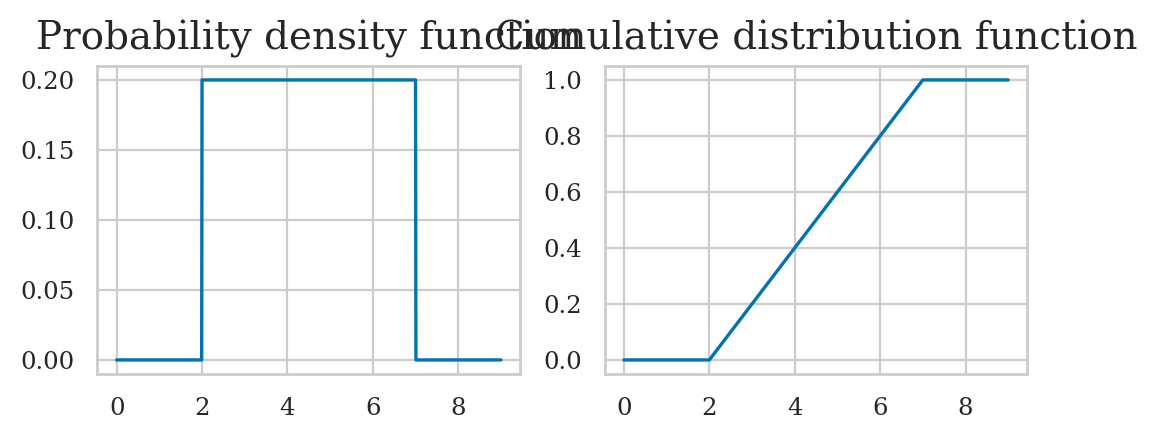
The uniform distribution \(\mathcal{U}(\alpha,\beta)\) is described by the following probability density function:
For a uniform distribution \(\mathcal{U}(\alpha,\beta)\), each \(x\) between \(\alpha\) and \(\beta\) is equally likely to occur, and values of \(x\) outside this range have zero probability of occurring.
from scipy.stats import uniform
alpha = 2
beta = 7
rvU = uniform(alpha, beta-alpha)
# draw 10 random samples from X
rvU.rvs(10)
array([3.87270059, 6.75357153, 5.65996971, 4.99329242, 2.7800932 ,
2.7799726 , 2.29041806, 6.33088073, 5.00557506, 5.54036289])
plot_pdf(rvU, xlims=[0,9]);
# # ALT. use sns.lineplot
# # plot the probability density function (pdf) of the random variable X
# xs = np.linspace(0, 10, 1000)
# fUs = rvU.pdf(xs)
# sns.lineplot(x=xs, y=fUs)
Cumulative distribution function#
plot_pdf_and_cdf(rvU, xlims=[0,9]);
Standard uniform distribution#
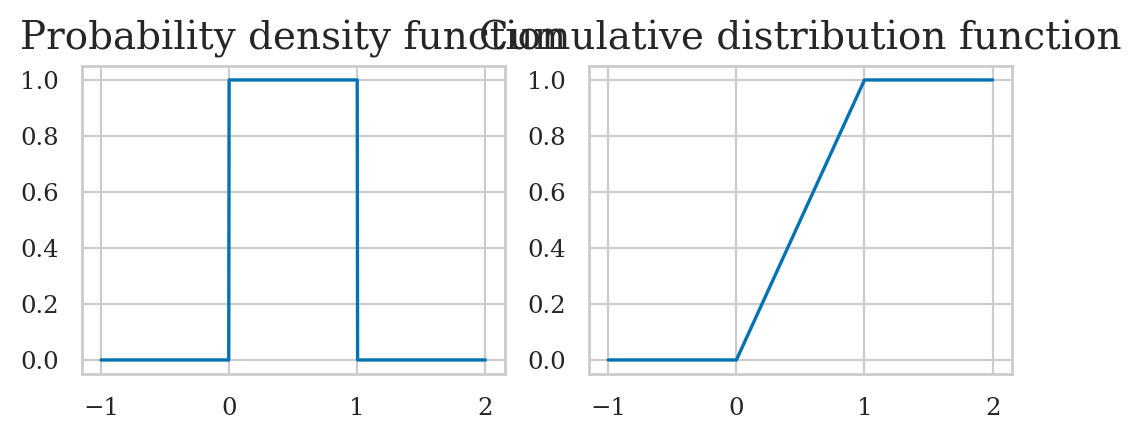
The standard uniform distribution \(U_s \sim \mathcal{U}(0,1)\) is described by the following probability density function:
where \(U\) is the name of the random variable and \(u\) are particular values it can take on.
The above equation describes tells you how likely it is to observe \(\{U_s=x\}\). For a uniform distribution \(\mathcal{U}(0,1)\), each \(x\) between 0 and 1 is equally likely to occur, and values of \(x\) outside this range have zero probability of occurring.
from scipy.stats import uniform
rvUs = uniform(0, 1)
# draw 10 random samples from X
rvUs.rvs(1)
array([0.02058449])
import random
random.seed(3)
random.random()
0.23796462709189137
random.uniform(0,1)
0.5442292252959519
import numpy as np
np.random.seed(42)
np.random.rand(10)
array([0.37454012, 0.95071431, 0.73199394, 0.59865848, 0.15601864,
0.15599452, 0.05808361, 0.86617615, 0.60111501, 0.70807258])
plot_pdf_and_cdf(rvUs, xlims=[-1,2]);
Simulating other random variables#
We can use the uniform random variable to generate random variables from other distributions.
For example,
suppose we want to generate observations of a coin toss random variable
which comes out heads 50% of the time and tails 50% of the time.
We can use the standard uniform random variables obtained from random.random()
and split the outcomes at the “halfway point” of the sample space,
to generate the 50-50 randomness of a coin toss.
The function flip_coin defined below shows how to do this:
def flip_coin():
u = random.random() # random number in [0,1]
if u < 0.5:
return "heads"
else:
return "tails"
# simulate one coin toss
flip_coin()
'heads'
# simulate 10 coin tosses
[flip_coin() for i in range(0,10)]
['tails',
'tails',
'heads',
'heads',
'tails',
'heads',
'heads',
'tails',
'heads',
'tails']
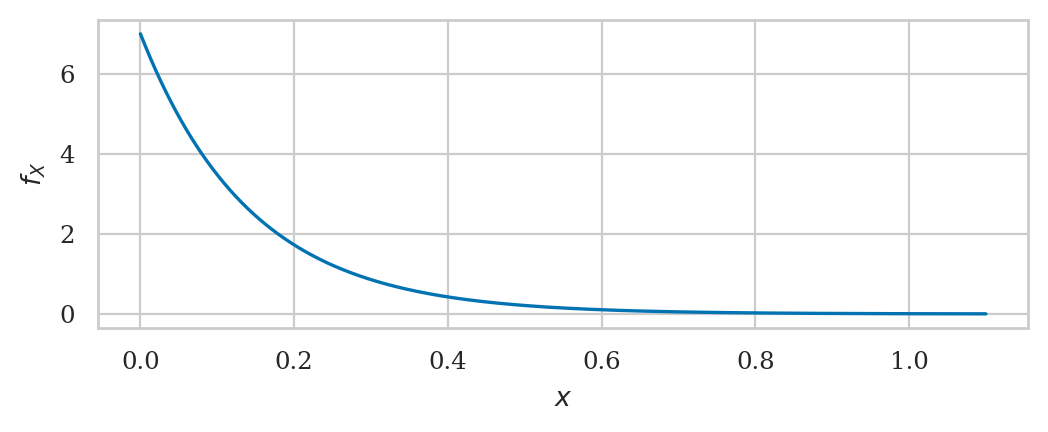
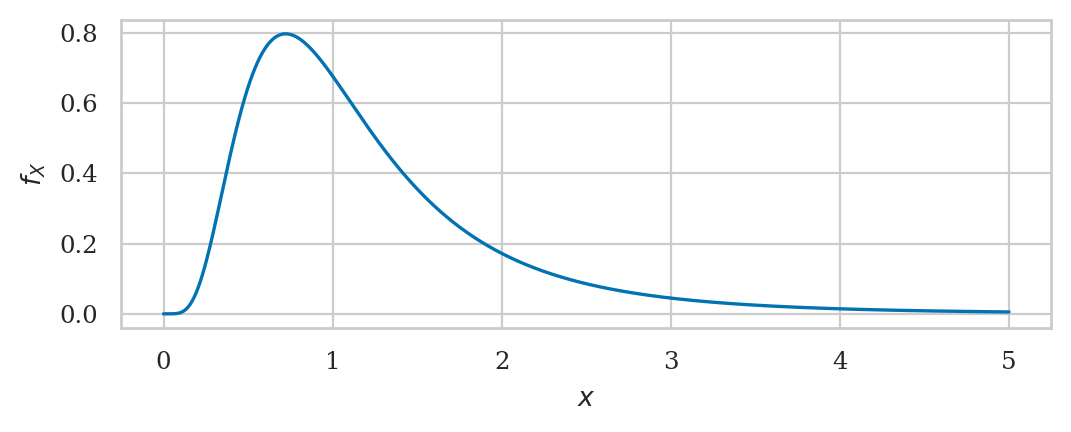
Exponential distribution#
from scipy.stats import expon
lam = 7
rvE = expon(loc=0, scale=1/lam)
The computer model expon accepts as its first argument an optional “location” parameter,
which can shift the exponential distribution to the right,
but we want loc=0 to get the simple case,
that corresponds to the un-shifted distribution \(\textrm{Expon}(\lambda)\).
rvE.mean(), rvE.var()
(0.14285714285714285, 0.02040816326530612)
# math formulas for mean and var
1/lam, 1/lam**2
(0.14285714285714285, 0.02040816326530612)
## ALT. we can obtain mean and ver using the .stats() method
## The code below also computes the skewness and the kurtosis
# mean, var, skew, kurt = rvE.stats(moments='mvsk')
# mean, var, skew, kurt
# f_E(5) = pdf value at x=10
rvE.pdf(0.2)
1.7261787475912451
plot_pdf(rvE, xlims=[0,1.1]);
Normal distribution#
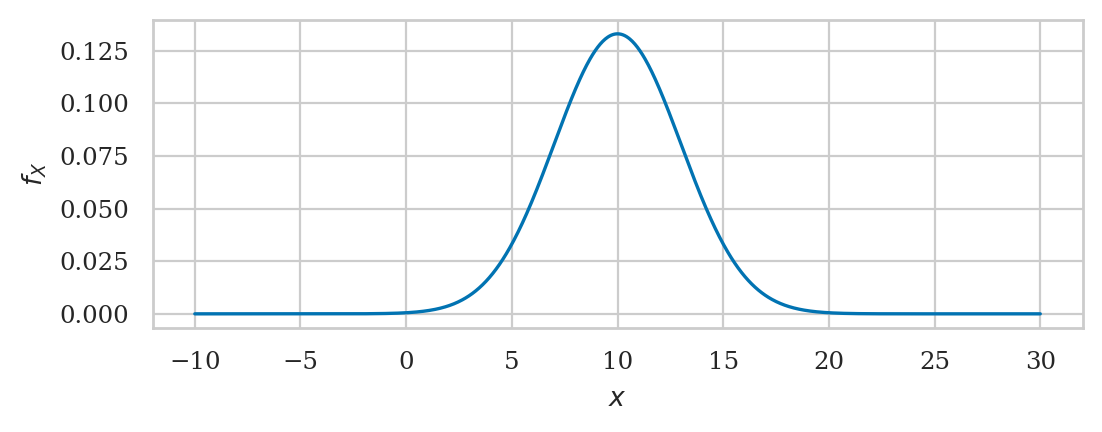
A random variable \(N\) with a normal distribution \(\mathcal{N}(\mu,\sigma)\) is described by the probability density function:
The mean \(\mu\) and the standard deviation \(\sigma\) are called the parameters of the distribution. The math notation \(\mathcal{N}(\mu, \sigma)\) is used to describe the whole family of normal probability distributions.
from scipy.stats import norm
mu = 10 # = 𝜇 where is the centre?
sigma = 3 # = 𝜎 how spread out is it?
rvN = norm(mu, sigma)
rvN.mean(), rvN.var()
(10.0, 9.0)
plot_pdf(rvN, xlims=[-10,30]);
# ALT. generate the plot manually
# create a normal random variable
from scipy.stats import norm
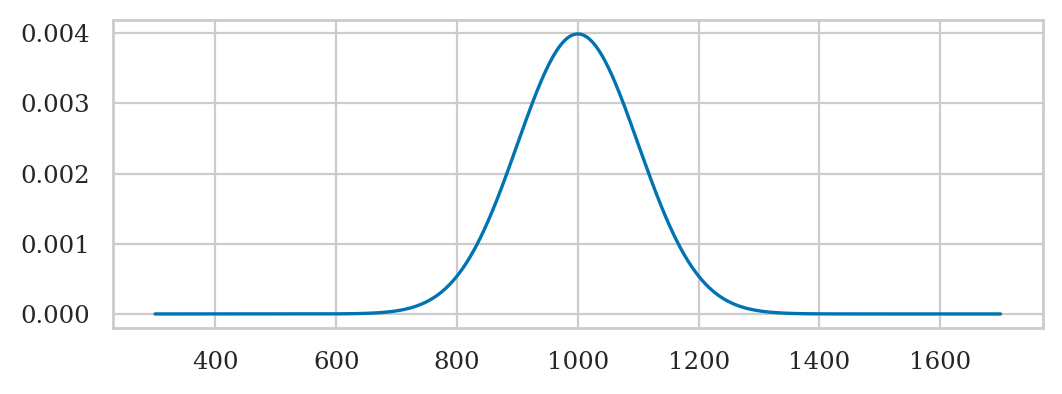
mean = 1000 # 𝜇 (mu) = where is its center?
std = 100 # 𝜎 (sigma) = how spread out is it?
rvN = norm(mean, std)
# plot its probability density function (pdf)
xs = np.linspace(300, 1700, 1000)
ys = rvN.pdf(xs)
ax = sns.lineplot(x=xs, y=ys)
Standard normal distribution#
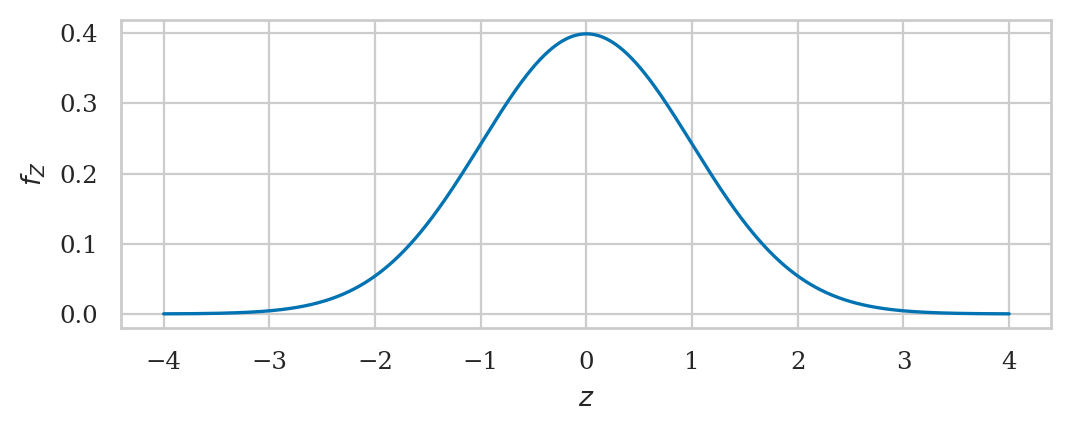
A standard normal is denoted \(Z\) with a normal distribution \(\mathcal{N}(\mu=0,\sigma=1)\) and described by the probability density function:
from scipy.stats import norm
rvZ = norm(0,1)
rvZ.mean(), rvZ.var()
(0.0, 1.0)
plot_pdf(rvZ, xlims=[-4,4], rv_name="Z");
Cumulative probabilities in the tails#
Probability of \(Z\) being smaller than \(-2.2\).
rvZ.cdf(-2.3)
0.010724110021675809
Probability of \(Z\) being greater than \(2.2\).
1 - rvZ.cdf(2.3)
0.010724110021675837
Probability of \(|Z| > 2.2\).
rvZ.cdf(-2.3) + (1-rvZ.cdf(2.3))
0.021448220043351646
norm.cdf(-2.3,0,1) + (1-norm.cdf(2.3,0,1))
0.021448220043351646
Inverse cumulative distribution calculations#
rvZ.ppf(0.05)
-1.6448536269514729
rvZ.ppf(0.95)
1.6448536269514722
rvZ.interval(0.9)
(-1.6448536269514729, 1.6448536269514722)
Mathematical interlude: the gamma function#
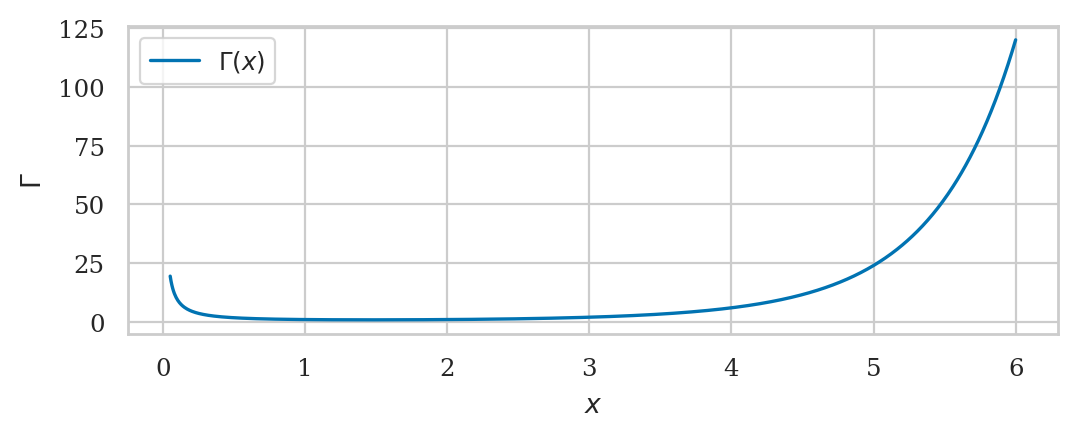
Gamma function#
from math import factorial
from scipy.special import gamma as gammaf
gammaf(1), factorial(0) # = 0! = 1
(1.0, 1)
gammaf(2), factorial(1) # = 1! = 1
(1.0, 1)
gammaf(3), factorial(2) # = 2! = 2*1
(2.0, 2)
gammaf(4), factorial(3) # = 3! = 3*2*1
(6.0, 6)
gammaf(5), factorial(4) # = 4! = 4*3*2*1
(24.0, 24)
gammaf(5.1)
27.93175373836837
factorial(4.1)
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[47], line 1
----> 1 factorial(4.1)
TypeError: 'float' object cannot be interpreted as an integer
[gammaf(x) for x in [5, 5.1, 5.5, 5.9, 6]]
[24.0, 27.93175373836837, 52.34277778455352, 101.27019121310353, 120.0]
# plot gammaf between 0 and 5
xs = np.linspace(0.05, 6, 1000)
fXs = gammaf(xs)
ax = sns.lineplot(x=xs, y=fXs, label="$\\Gamma(x)$")
ax.set_xlabel("$x$")
ax.set_ylabel(r"$\Gamma$")
Text(0, 0.5, '$\\Gamma$')
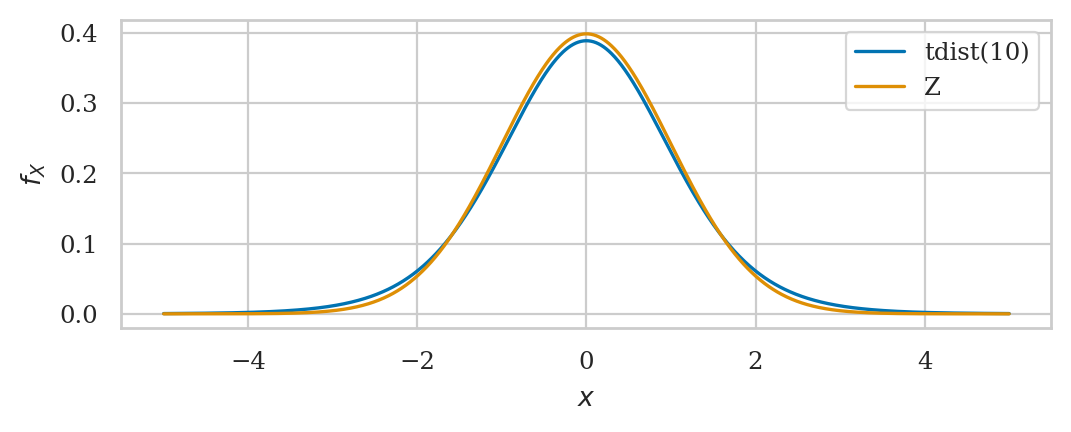
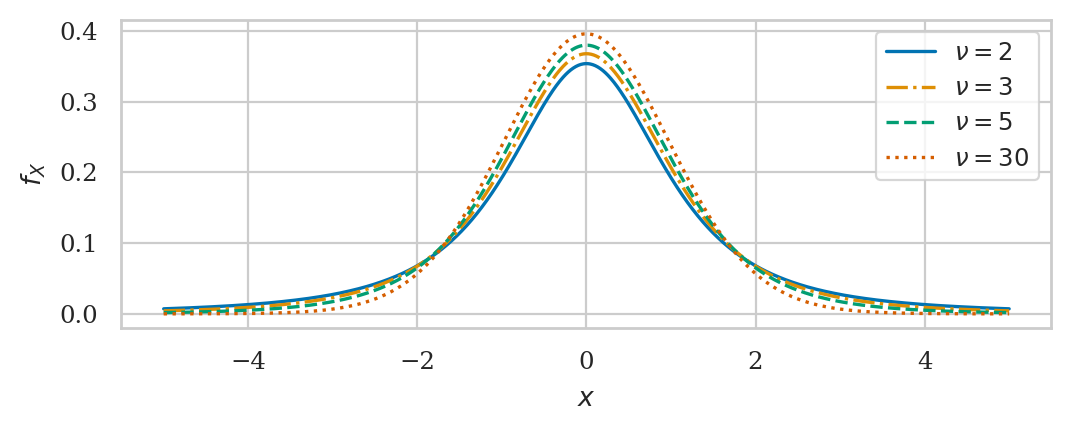
Student’s t-distribution#
This is a generalization of the standard normal with “heavy” tails.
from scipy.stats import t as tdist
rvT = tdist(df=10)
ax = plot_pdf(rvT, xlims=[-5,5], label=f"tdist(10)")
plot_pdf(rvZ, xlims=[-5,5], ax=ax, label="Z");
rvT.mean(), rvT.var()
(0.0, 1.25)
# Kurtosis formula kurt(rvT) = 6/(df-4) for df>4
rvT.stats("k")
1.0
rvT.cdf(-2.3)
0.022127156642143552
rvT.ppf(0.05), rvT.ppf(0.95)
(-1.8124611228107341, 1.8124611228107335)
fig, ax = plt.subplots()
linestyles = ['solid', 'dashdot', 'dashed', 'dotted']
for i, df in enumerate([2,3,5,30]):
rvT = tdist(df)
linestyle = linestyles[i]
plot_pdf(rvT, xlims=[-5,5], ax=ax, label="$\\nu={}$".format(df), linestyle=linestyle)
Fisher–Snedecor’s F-distribution#
from scipy.stats import f as fdist
df1, df2 = 15, 10
rvF = fdist(df1, df2)
rvF.mean(), rvF.var()
(1.25, 0.7986111111111112)
plot_pdf(rvF, xlims=[0,5]);
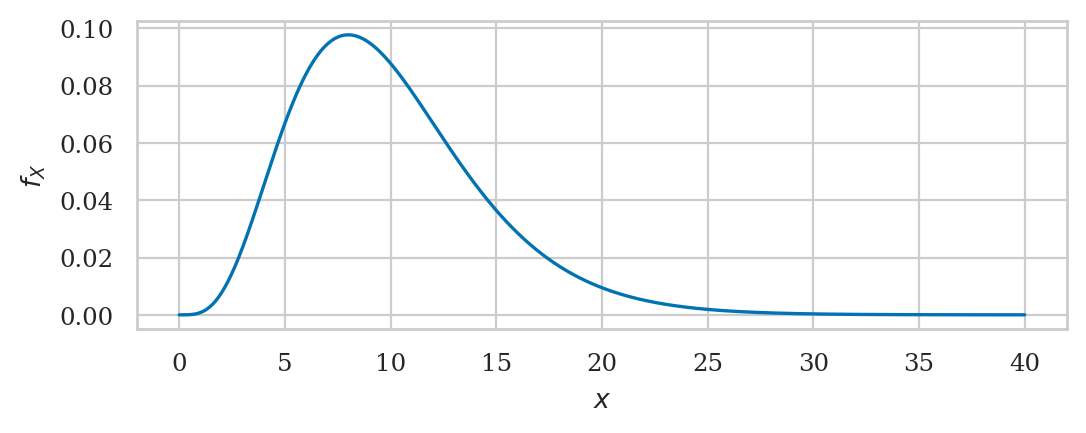
Chi-squared distribution#
from scipy.stats import chi2
df = 10
rvX2 = chi2(df)
rvX2.mean(), rvX2.var()
(10.0, 20.0)
1 - rvX2.cdf(20)
0.02925268807696113
plot_pdf(rvX2, xlims=[0,40]);
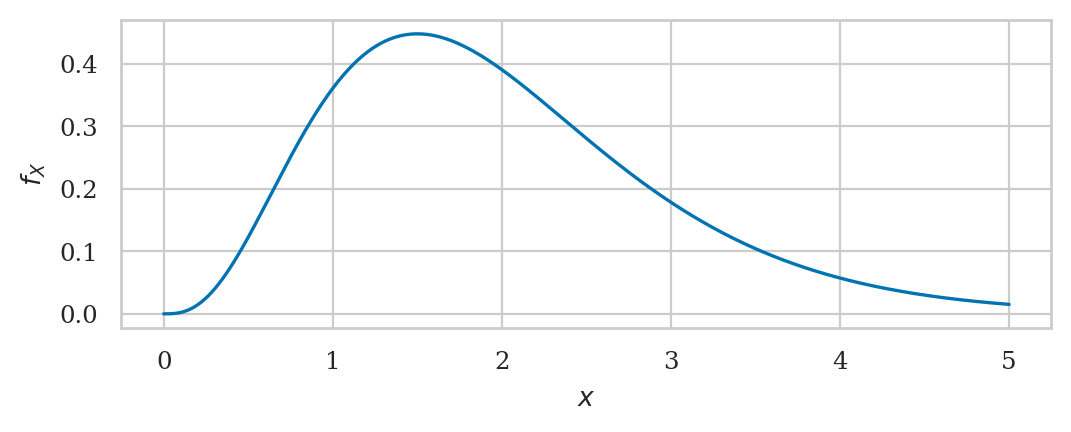
Gamma distribution#
https://en.wikipedia.org/wiki/Gamma_distribution
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.gamma.html
from scipy.stats import gamma as gammadist
alpha = 4
loc = 0
lam = 2
beta = 1/lam
rvG = gammadist(alpha, loc, beta)
rvG.mean(), rvG.var()
(2.0, 1.0)
plot_pdf(rvG, xlims=[0,5]);
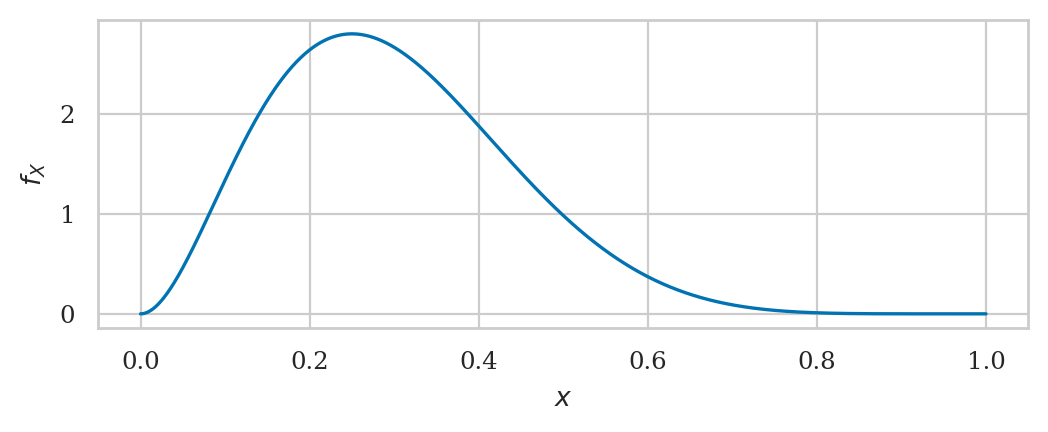
Beta distribution#
from scipy.stats import beta as betadist
alpha = 3
beta = 7
rvB = betadist(alpha, beta)
rvB.mean(), rvB.var()
(0.3, 0.019090909090909092)
plot_pdf(rvB, xlims=[0,1]);
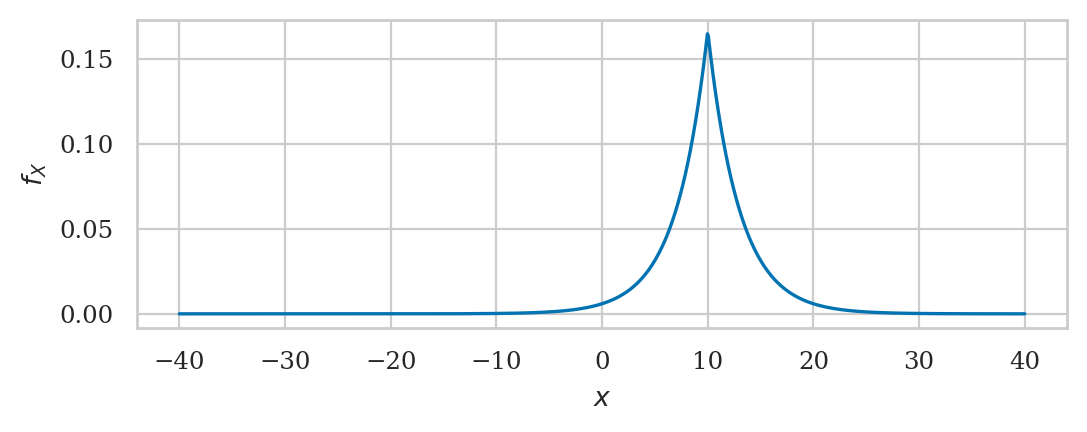
Laplace distribution#
from scipy.stats import laplace
mu = 10
b = 3
rvL = laplace(mu, b)
rvL.mean(), rvL.var()
(10.0, 18.0)
plot_pdf(rvL, xlims=[-40,40]);
Explanations#
Location-scale families#
Normal location-scale family#
b = 109
muN = 100
sigmaN = 5
# standardize b
z_b = (b - muN) / sigmaN
z_b
1.8
from scipy.stats import norm
rvZ = norm(loc=0, scale=1)
1 - rvZ.cdf(z_b)
0.03593031911292577
rvN = norm(loc=100, scale=5)
1 - rvN.cdf(b)
0.03593031911292577
Student’s t location-scale family#
b = 109
locS = 100
scaleS = 5
t_b = (b - locS) / scaleS
t_b
1.8
from scipy.stats import t as tdist
rvT = tdist(df=6, loc=0, scale=1)
1 - rvT.cdf(t_b)
0.06097621069194392
rvS = tdist(df=6, loc=100, scale=5)
1 - rvS.cdf(b)
0.06097621069194392
Uniform location-scale family#
locV = 100
scaleV = 20
b = 115
u_b = (b - locV) / scaleV
u_b
0.75
from scipy.stats import uniform
rvU = uniform(0, 1)
1 - rvU.cdf(u_b)
0.25
rvV = uniform(100, 20)
1 - rvV.cdf(115)
0.25
Chi-square scale family#
scaleS = 10
b = 150
q_b = 150 / scaleS
from scipy.stats import chi2
rvQ = chi2(df=7)
1 - rvQ.cdf(q_b)
0.03599940476342878
rvS = chi2(df=7, scale=10)
1 - rvS.cdf(150)
0.03599940476342878