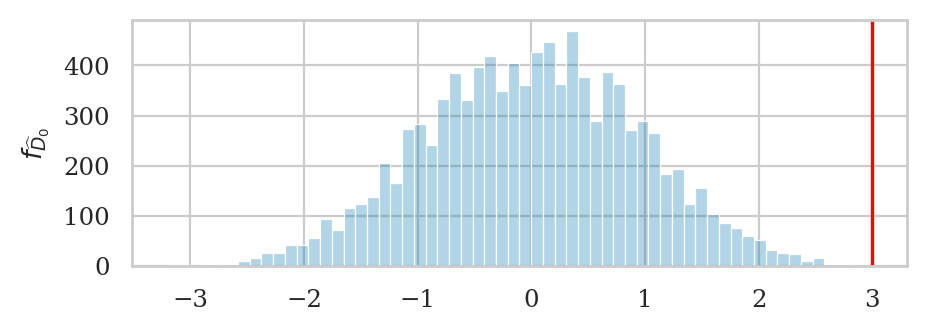Section 3.5 — Two-sample hypothesis tests

Section 3.5 — Two-sample hypothesis tests#

This notebook contains the code examples from Section 3.5 Two-sample hypothesis tests of the No Bullshit Guide to Statistics.

Notebook setup#

# load Python modules
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Plot helper functions
from ministats import nicebins
from ministats import plot_pdf
from ministats.utils import savefigure

# Stats helper functions
from ministats import tailvalues
from ministats import tailprobs

# Figures setup
plt.clf()  # needed otherwise `sns.set_theme` doesn't work
from plot_helpers import RCPARAMS
# RCPARAMS.update({'figure.figsize': (10, 3)})   # good for screen
RCPARAMS.update({'figure.figsize': (5, 1.6)})  # good for print
sns.set_theme(
    context="paper",
    style="whitegrid",
    palette="colorblind",
    rc=RCPARAMS,
)

# Useful colors
snspal = sns.color_palette()
blue, orange, purple = snspal[0], snspal[1], snspal[4]
# red = sns.color_palette("tab10")[3]

# High-resolution please
%config InlineBackend.figure_format = 'retina'

# Where to store figures
DESTDIR = "figures/stats/two_sample_tests"

<Figure size 640x480 with 0 Axes>

# set random seed for repeatability
np.random.seed(42)

$\def\stderr#1{\mathbf{se}_{#1}}$ $\def\stderrhat#1{\hat{\mathbf{se}}_{#1}}$ $\newcommand{\Mean}{\textbf{Mean}}$ $\newcommand{\Var}{\textbf{Var}}$ $\newcommand{\Std}{\textbf{Std}}$ $\newcommand{\Freq}{\textbf{Freq}}$ $\newcommand{\RelFreq}{\textbf{RelFreq}}$ $\newcommand{\DMeans}{\textbf{DMeans}}$ $\newcommand{\Prop}{\textbf{Prop}}$ $\newcommand{\DProps}{\textbf{DProps}}$

\[ \newcommand{\CI}[1]{\textbf{CI}_{#1}} \newcommand{\CIL}[1]{\textbf{L}_{#1}} \newcommand{\CIU}[1]{\textbf{U}_{#1}} \newcommand{\ci}[1]{\textbf{ci}_{#1}} \newcommand{\cil}[1]{\textbf{l}_{#1}} \newcommand{\ciu}[1]{\textbf{u}_{#1}} \]

(this cell contains the macro definitions like $\stderr{\overline{\mathbf{x}}}$, $\stderrhat{}$, $\Mean$, …)

Definitions#

Populations. We’ll label the two unknown populations $X$ and $Y$. and assume the arbitrary model family $\mathcal{M}$ with mean parameter $X \sim \mathcal{M}(\mu_X)$ and $Y \sim \mathcal{M}(\mu_Y)$.
Parameters. The means of the two populations $\mu_X$ and $\mu_Y$ are unknown, and what we want to study…
Samples. We assume the two samples $\mathbf{x} = (x_1, x_2, \ldots, x_n)$ and $\mathbf{y} = (y_1, y_2, \ldots, y_m)$ are randomly selected from the populations $X$ and $Y$.
Estimate (statistic) $\hat{d} = \overline{\mathbf{x}} - \overline{\mathbf{y}}$: the difference between means of the two samples $\mathbf{x}$ and $\mathbf{y}$.
Estimator $\DMeans$: the function that computes the difference between means from two samples, $\hat{d} = \DMeans(\mathbf{x},\mathbf{y}) = \overline{\mathbf{x}} - \overline{\mathbf{y}}$. the function we use to compute the estimate $\hat{d}$.
Sampling distribution $\hat{D} = \DMeans(\mathbf{X}, \mathbf{Y})$: the difference between means computed from two random samples $\mathbf{X}$ and $\mathbf{Y}$.

def mean(sample):
    return sum(sample) / len(sample)

def var(sample):
    xbar = mean(sample)
    sumsqdevs = sum([(xi-xbar)**2 for xi in sample])
    return sumsqdevs / (len(sample)-1)

def std(sample):
    s2 = var(sample)
    return np.sqrt(s2)

def dmeans(xsample, ysample):
    dhat = mean(xsample) - mean(ysample)
    return dhat

Comparing two groups#

Description of the problem: compare two group based on sample means computed from each group.

Computing $p$-values#

filename = os.path.join(DESTDIR, "panel_D0_hist_and_dist_twosided_pvalues.pdf")

from scipy.stats import t as tdist
rvT = tdist(df=9)

xs = np.linspace(-4, 4, 1000)
ys = rvT.pdf(xs)

N = 100000
np.random.seed(42)
ts = rvT.rvs(N)

bins = nicebins(xs, 2, nbins=50)


with plt.rc_context({"figure.figsize":(7,2)}), sns.axes_style("ticks"):
    fig, (ax1, ax2) = plt.subplots(1,2)

    # D0 hist
    sns.histplot(ts, ax=ax1, bins=bins, alpha=0.3)
    ax1.set_title("(a) permutation test")
    ax1.set_xlim(-4, 4)
    ax1.set_xticks([2])
    ax1.set_xticklabels([])
    ax1.set_yticks([])
    ax1.set_ylabel("$f_{\widehat{D}_0}$")
    # highlight the left and right tails
    tailvaluesl = [t for t in ts if t <= -2]
    sns.histplot(tailvaluesl, bins=bins, ax=ax1, color="red")
    ax1.text(-2.3, -630, "$-|\hat{d}|$", verticalalignment="top", horizontalalignment="center")
    tailvaluesr = [t for t in ts if t >= 2]
    sns.histplot(tailvaluesr, bins=bins, ax=ax1, color="red")
    ax1.text(2, -630, "$|\hat{d}|$", verticalalignment="top", horizontalalignment="center")
    # ax1.axvline(2, color="red")

    
    # D0 dist
    sns.lineplot(x=xs, y=ys, ax=ax2)
    ax2.set_title("(b) analytical apprixmation")
    ax2.set_xlim(-4, 4)
    ax2.set_ylim(0, 0.42)
    ax2.set_xticks([-2,2])
    ax2.set_xticklabels([])
    ax2.set_yticks([])
    ax2.set_ylabel("$f_{\widehat{D}_0}$")
    # highlight the left and right tails
    mask = (xs < -2)
    ax2.fill_between(xs[mask], y1=ys[mask], alpha=0.6, facecolor="red")
    ax2.text(-2, -0.03, r"$-|\hat{d}|$", verticalalignment="top", horizontalalignment="center")
    mask = (xs > 2)
    ax2.fill_between(xs[mask], y1=ys[mask], alpha=0.6, facecolor="red")
    ax2.text(2, -0.03, r"$|\hat{d}|$", verticalalignment="top", horizontalalignment="center")

savefigure(fig, filename, tight_layout_kwargs={"w_pad":5})

Saved figure to figures/stats/two_sample_tests/panel_D0_hist_and_dist_twosided_pvalues.pdf
Saved figure to figures/stats/two_sample_tests/panel_D0_hist_and_dist_twosided_pvalues.png

../_images/fe3d3268a9f9d22cf2548399fb6445ef284cfa75957ee259fc26f99dfb3334b2.png

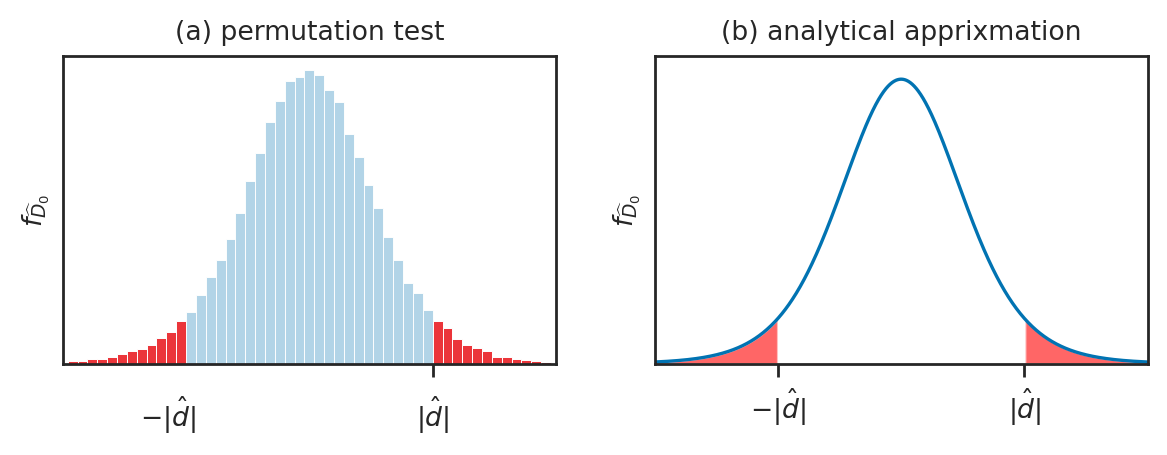
Permutation test for comparing two populations#

The permutations test is a computational approach for comparing two group. The permutation test takes it’s name from the action of mixing up the group-membership labels and computing a statistic which is a way to generate samples from the null hypothesis in situations where the null hypothesis states there is no difference between two groups.

Permutations#

np.random.seed(43)
np.random.permutation([1,2,3,4,5,6,7])

array([4, 6, 3, 7, 2, 1, 5])

np.random.seed(45)
np.random.permutation([1,2,3,4,5,6,7])

array([6, 3, 2, 1, 5, 7, 4])

Resampling under the null hypothesis#

def resample_under_H0(xsample, ysample):
    """
    Generate new samples from a random permutation of
    the values in the samples `xsample` and `xsample`.
    """
    values = np.concatenate((xsample, ysample))
    pvalues = np.random.permutation(values)
    pxsample = pvalues[0:len(xsample)]
    pysample = pvalues[len(xsample):]
    return pxsample, pysample

# example 1
np.random.seed(43)
resample_under_H0([1,2,3], [4,5,6,7])

(array([4, 6, 3]), array([7, 2, 1, 5]))

# example 2
np.random.seed(45)
resample_under_H0([1,2,3], [4,5,6,7])

(array([6, 3, 2]), array([1, 5, 7, 4]))

The function resample_under_H0 gives us a way to generate samples from the null hypothesis. We can then compute the value of the dmeans statistic for these samples. We used the assumption of “no difference” under the null hypothesis, and translated this to the “forget the labels” interpretation.

Example 5P: electricity prices#

The probability model under the alternative hypothesis describes two populations with different parameters:

\[ H_A: \qquad X_W = \mathcal{N}(\color{blue}{\mu_W}, \sigma_W) \quad \textrm{and} \quad X_{E} = \mathcal{N}(\color{orange}{\mu_{E}}, \sigma_{E}) \]

Under the null hypothesis the populations have the same mean:

\[ H_0: \qquad X_W = \mathcal{N}(\color{red}{\mu_0}, \sigma_W) \quad \textrm{and} \quad X_{E} = \mathcal{N}(\color{red}{\mu_0}, \sigma_{E}) \]

eprices = pd.read_csv("../datasets/eprices.csv")
# eprices

eprices.groupby("loc")["price"].describe()

	count	mean	std	min	25%	50%	75%	max
loc
East	9.0	6.155556	0.877655	4.8	5.5	6.3	6.5	7.7
West	9.0	9.155556	1.562139	6.8	8.3	8.6	10.0	11.8

pricesW = eprices[eprices["loc"]=="West"]["price"]
pricesE = eprices[eprices["loc"]=="East"]["price"]

# 1. Calculate the observed difference between means
dprice = dmeans(pricesW, pricesE)
dprice

3.0

Our goal is to determine how likely or unlikely the observed value $\hat{d}=3$ is under the null hypothesis $H_0$. This means we need to obtain the sampling distribution of $\hat{D}$ under $H_0$, which we can do using the permutation test.

Let’s look at some of the differences we can expect to observe under $H_0$.

#######################################################
np.random.seed(31)
# generate new samples by shuffling the labels
ppricesW, ppricesE = resample_under_H0(pricesW, pricesE)

# Compute the difference in means for the bootstrap samples
pdhat0 = dmeans(ppricesW, ppricesE)
pdhat0

1.6444444444444475

Running a permutation test#

We can repeat the resampling procedure 10000 times to get the sampling distribution of $\widehat{D}_0$ under $H_0$, as illustrated in the code procedure below.

np.random.seed(42)

# 2. Obtain the sampling distribution under H0
P = 10000
pdhats0 = []
for i in range(0, P):
    ps1, ps2 = resample_under_H0(pricesW, pricesE)
    pdhat0 = dmeans(ps1, ps2)
    pdhats0.append(pdhat0)

Now that we have the sampling distribution $\widehat{D}_0$, we can see where the observed value $\hat{d}= 3$ =dprice falls within this distribution. The $p$-value is the probability of observing value dprice=3 or more extreme under the null hypothesis.

# 3. Compute the p-value 
tails = tailvalues(pdhats0, dprice)
pvalue = len(tails) / len(pdhats0)
pvalue

0.0002

filename = os.path.join(DESTDIR, "hist_p-value_dmeans_eprices.pdf")

# plot the sampling distribution in blue
bins = nicebins(pdhats0, dprice)
ax = sns.histplot(pdhats0, bins=bins, alpha=0.3)

# plot red line for the observed statistic
plt.axvline(dprice, color="red")

# plot the values that are equal or more extreme in red
sns.histplot(tails, ax=ax, bins=bins, color="red")
ax.set_ylabel("$f_{\widehat{D}_0}$")

savefigure(ax, filename)

Saved figure to figures/stats/two_sample_tests/hist_p-value_dmeans_eprices.pdf

Saved figure to figures/stats/two_sample_tests/hist_p-value_dmeans_eprices.png

../_images/978fb77f610373cb61914053c688599908c374eac88dd9c81393f9b4f530f704.png

Effect size estimates#

dprice = dmeans(pricesW, pricesE)
dprice

3.0

The bootstrap confidence interval for the effect size $\ci{\Delta,0.9}^*$ tells us a range of plausible values for the effect size.

from ministats import ci_dmeans

np.random.seed(45)
ci_dmeans(pricesW, pricesE, alpha=0.1, method="b")

[2.0777777777777775, 3.9555555555555557]

The 90% confidence interval $\ci{\Delta,0.9}^* = [2.08, 3.96]$ describes an interval of numbers that should contain the difference between group means $\Delta$ at least 90% of the time:

\[ \textrm{Pr}_{\mathbf{X}}\big(\{ \Delta \in \ci{\Delta,0.9}^* \}\big) \geq 0.9. \]

Reusable function#

def permutation_test_dmeans(xsample, ysample, P=10000):
    # 1. Compute the observed difference between means
    obsdhat = dmeans(xsample, ysample)

    # 2. Get sampling dist. of `dmeans` under H0
    pdhats0 = []
    for i in range(0, P):
        psx, psy = resample_under_H0(xsample, ysample)
        pdhat0 = dmeans(psx, psy)
        pdhats0.append(pdhat0)

    # 3. Compute the p-value
    tails = tailvalues(pdhats0, obsdhat, alt="two-sided")
    pvalue = len(tails) / len(pdhats0)
    return pvalue

np.random.seed(42)

permutation_test_dmeans(pricesW, pricesE)

0.0002

Example 6P: lecture and debate curriculums#

students = pd.read_csv("../datasets/students.csv")
# students

students.groupby("curriculum")["score"].describe()

	count	mean	std	min	25%	50%	75%	max
curriculum
debate	8.0	76.462500	10.519633	62.9	69.55	75.55	80.925	96.2
lecture	7.0	68.142857	7.758406	57.0	63.30	70.30	73.850	75.4

studentsD = students[students["curriculum"]=="debate"]
studentsL = students[students["curriculum"]=="lecture"]
scoresD = studentsD["score"]
scoresL = studentsL["score"]

# observed difference between score means
dscore = dmeans(scoresD, scoresL)
dscore

8.319642857142853

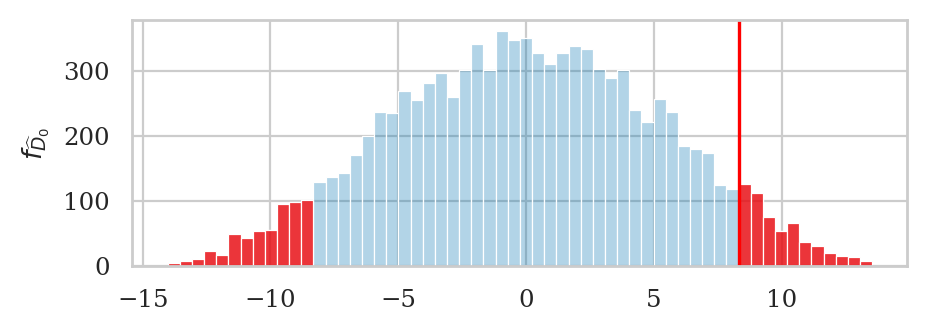
Our goal is to determine how likely or unlikely this observed value $\hat{d}_s=8.32$ is under the null hypothesis $H_0$. This means we need to obtain the sampling distribution of $\hat{D}_0$ under $H_0$, which we can do using the permutation test.

np.random.seed(43)
pvalue = permutation_test_dmeans(scoresD, scoresL)
pvalue

0.1118

# FIGURES ONLY
filename = os.path.join(DESTDIR, "hist_p-value_dmeans_students.pdf")

# generate sampling distribution under H0
np.random.seed(43)
pdhats = []
P = 10000
for i in range(0, P):
    rs1, rs2 = resample_under_H0(scoresD, scoresL)
    pdhat = dmeans(rs1, rs2)
    pdhats.append(pdhat)
    
# plot the sampling distribution in blue
bins = nicebins(pdhats, dscore)
ax = sns.histplot(pdhats, bins=bins, alpha=0.3)

# plot red line for the observed statistic
plt.axvline(dscore, color="red")

# plot the values that are equal or more extreme in red
tails = tailvalues(pdhats, dscore)
# print( len(tails) / len(pdhats) )
sns.histplot(tails, bins=bins, ax=ax, color="red")
ax.set_ylabel("$f_{\widehat{D}_0}$")

savefigure(ax, filename)

Saved figure to figures/stats/two_sample_tests/hist_p-value_dmeans_students.pdf

Saved figure to figures/stats/two_sample_tests/hist_p-value_dmeans_students.png

../_images/c66bb4ea088c797e97578027f608ddf6ca2bff5345af680acc73b7d1bfa2c356.png

Analytical approximation methods#

We’ll now look at another approach for computing the sampling distribution of the difference between means estimator, using an analytical approximations based on Student’s $t$-distribution. This is called the “two-sample $t$-test” and it is procedure most commonly taught approach in STATS 101 courses.

How likely or unlikely is the observed difference $d=3$ under the null hypothesis $H_0$?

Analytical approximations are math models for describing the sampling distribution under $H_0$
- Real sampling distributions: obtained by repeated sampling from $H_0$
- Analytical approximation: math model based on estimated parameters
Based on this assumption we can use the theoretical model for the difference between group means (we assumed the two unknown populations are normally distributed), we can obtain a closed form expression for the sampling distribution of $D_0$.
In particular, the probability model for the two groups under $H_0$ are:

\[ H_0: \qquad X = \mathcal{N}({\color{red}{\mu_0}}, \sigma_X) \quad \textrm{and} \quad Y = \mathcal{N}({\color{red}{\mu_0}}, \sigma_Y), \quad \]

from which we can derive the model for $D = \overline{\mathbf{X}} - \overline{\mathbf{Y}}$:

\[ D_0 \sim \mathcal{N}\!\left( {\color{red}{0}}, \; \stderr{\hat{d}} \right) \]

In words, the sampling distribution of the difference between group means is normally distributed with mean $\Delta = 0$ and standard deviation $\stderrhat{\hat{d}}$, described by the formula:

\[ \stderr{\hat{d}} % \; = \; \sqrt{ \stderr{\overline{\mathbf{x}}}^2 + \stderr{\overline{\mathbf{y}}}^2 } = \sqrt{ \tfrac{\sigma_X^2}{n} + \tfrac{\sigma_Y^2}{m} }\;. \]

The standard error of the difference between means depends on the variance of the two groups $\sigma_X^2$ and $\sigma_Y^2$. Recall we’ve seen this expression earlier in Section 3.1 and Section 3.2 as well.

Problem 1: the population variances $\sigma_X^2$ and $\sigma_Y^2$ are unknown, and we only have the estimated variances $s_{\mathbf{x}}$ and $s_{\mathbf{y}}$, which we calculated from the samples $\mathbf{x}$ and $\mathbf{y}$.
Solution 1: use plug in estimate and We can obtain an approximation to the standard error of the difference between means estimator using the plug-in principle, which states we can use search-and-replace the population parameters $\sigma_X^2$ and $\sigma_Y^2$ with the estimates $s_{\mathbf{x}}$ and $s_{\mathbf{y}}$:

\[ \stderrhat{\hat{d}} % \; = \; \sqrt{ \stderrhat{\overline{\mathbf{x}}}^2 + \stderrhat{\overline{\mathbf{y}}}^2 } = \sqrt{ \tfrac{s_{\mathbf{x}}^2}{n} + \tfrac{s_{\mathbf{y}}^2}{m} }\;. \]
Problem 2: the estimated standard error $\stderrhat{\hat{d}}$ tends to underestimate the true standard error $\stderr{\hat{d}}$, so when we use the basic normal model $\mathcal{N}\!\left(\tt{loc}=0, \tt{scale}=\stderrhat{\hat{d}} \right)$ the approximation is off (not enough weight in the tails).
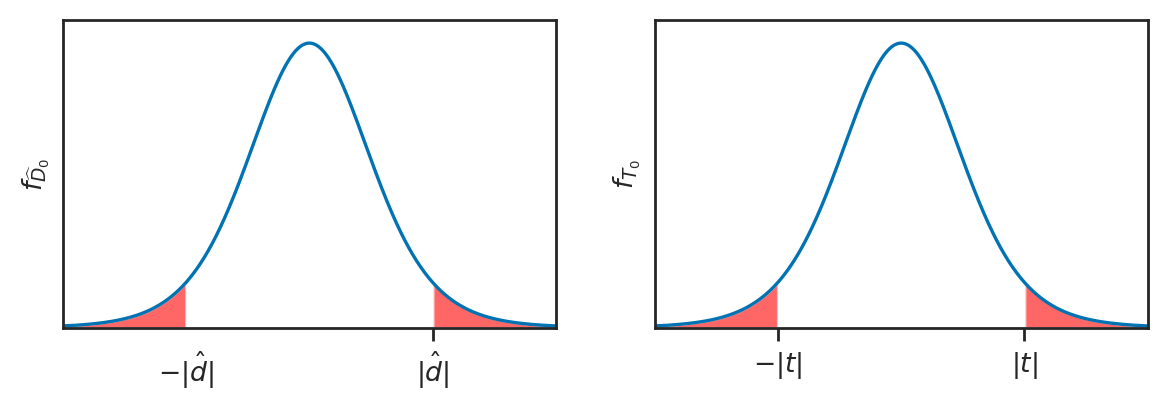
Solution 2: use Student’s $t$-distribution. We can define a new model for the $D_0 = \overline{\mathbf{X}} - \overline{\mathbf{Y}}$ based on Student’s $t$-distribution: $$ D_0 \sim \mathcal{T}\!\left(\tt{df}=\nu_d, \; \tt{loc}={\color{red}{0}}, \; \tt{scale}=\stderrhat{\hat{d}} \right) $$ In words, the sampling distribution of the difference between group means can be modeled as Student's $t$-distribution with $\nu_d$ degrees of freedom, centered at $0$, with scale parameter $\stderrhat{\hat{d}}$.
The degrees of freedom parameter, denoted $\nu_d$ (Greek letter nu) in equations (df in code) determines the “weight” in the tails of the distribution. It is computed by a complicated formula that depends on the sample sizes $n$ and $m$, and the sample standard deviations $s_{\mathbf{x}}$ and $s_{\mathbf{y}}$.

filename = os.path.join(DESTDIR, "panel_D0_and_T0_twosided_pvalues.pdf")

from scipy.stats import t as tdist
rvT = tdist(df=9)
xs = np.linspace(-4, 4, 1000)
ys = rvT.pdf(xs)

with plt.rc_context({"figure.figsize":(7,2)}), sns.axes_style("ticks"):
    fig, (ax1, ax2) = plt.subplots(1,2)

    # D0
    sns.lineplot(x=xs, y=ys, ax=ax1)
    ax1.set_xlim(-4, 4)
    ax1.set_ylim(0, 0.42)
    ax1.set_xticks([2])
    ax1.set_xticklabels([])
    ax1.set_yticks([])
    ax1.set_ylabel("$f_{\widehat{D}_0}$")
    # highlight the left and right tails
    mask = (xs < -2)
    ax1.fill_between(xs[mask], y1=ys[mask], alpha=0.6, facecolor="red")
    ax1.text(-2, -0.03, r"$-|\hat{d}|$", verticalalignment="top", horizontalalignment="center")
    mask = (xs > 2)
    ax1.fill_between(xs[mask], y1=ys[mask], alpha=0.6, facecolor="red")
    ax1.text(2, -0.03, r"$|\hat{d}|$", verticalalignment="top", horizontalalignment="center")

    # T0
    sns.lineplot(x=xs, y=ys, ax=ax2)
    ax2.set_xlim(-4, 4)
    ax2.set_ylim(0, 0.42)
    ax2.set_xticks([-2,2])
    ax2.set_xticklabels([])
    ax2.set_yticks([])
    ax2.set_ylabel("$f_{T_0}$")
    # highlight the left and right tails
    mask = (xs < -2)
    ax2.fill_between(xs[mask], y1=ys[mask], alpha=0.6, facecolor="red")
    ax2.text(-2, -0.03, r"$-|t|$", verticalalignment="top", horizontalalignment="center")
    mask = (xs > 2)
    ax2.fill_between(xs[mask], y1=ys[mask], alpha=0.6, facecolor="red")
    ax2.text(2, -0.03, r"$|t|$", verticalalignment="top", horizontalalignment="center")

savefigure(fig, filename, tight_layout_kwargs={"w_pad":5})

Saved figure to figures/stats/two_sample_tests/panel_D0_and_T0_twosided_pvalues.pdf
Saved figure to figures/stats/two_sample_tests/panel_D0_and_T0_twosided_pvalues.png

../_images/9a09145809635bc7c3f57dfbf7f1ec1f7bfc0642cdf407a02f79e4b8b5dbf23c.png

Example 5T: comparing East and West electricity prices#

eprices = pd.read_csv("../datasets/eprices.csv")
pricesW = eprices[eprices["loc"]=="West"]["price"]
pricesE = eprices[eprices["loc"]=="East"]["price"]

# Calculate the observed difference between means
dprice = dmeans(pricesW, pricesE)
dprice

3.0

Two-sample t-test#

We’ll now show the data, probability modeling, and calculation steps of the “two-sample $t$-test for comparing group means. The two-sample $t$-test is also known as Welch’s t-test.

# Calculate the sample size and the standard deviation for each group
nW, nE = len(pricesW), len(pricesE)
stdW, stdE = std(pricesW), std(pricesE)

# Compute the standard error of the estimator D
seD = np.sqrt(stdW**2/nW + stdE**2/nE)
seD

0.5972674401486561

# Compute the value of the t-statistic
obst = (dprice - 0) / seD
obst

5.022875513276463

from ministats import calcdf
    
# Obtain the degrees of freedom from the crazy formula
dfD = calcdf(stdW, nW, stdE, nE)
dfD

12.59281702723103

# Calculate the p-value

from scipy.stats import t as tdist
rvT0 = tdist(df=dfD)
from ministats import tailprobs
pvalue = tailprobs(rvT0, obst, alt="two-sided")
pvalue

0.00025703383372176864

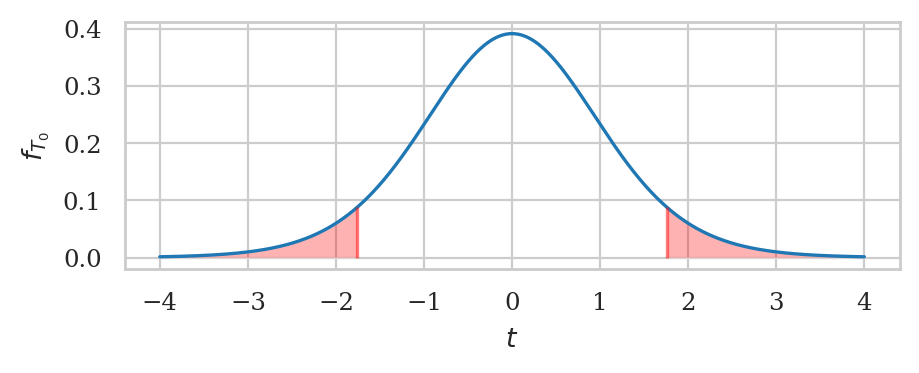
# # SKIP BECAUSE TOO SMALL
# filename = os.path.join(DESTDIR, "rvT0_p-value_dmeans_eprices.pdf")
# from ministats import calc_prob_and_plot_tails
# _, ax = calc_prob_and_plot_tails(rvT0, -obst, obst, xlims=[-4,4])
# ax.set_title(None)
# ax.set_xlabel("$t$")
# ax.set_ylabel("$f_{T_0}$")
# savefigure(ax, filename)

Effect size estimates#

dprice = dmeans(pricesW, pricesE)
dprice

3.0

The confidence interval for the effect size $\ci{\Delta,0.9}$ tells us a range of plausible values for the effect size.

from ministats import ci_dmeans

ci_dmeans(pricesW, pricesE, alpha=0.1, method="a")

[1.9396575883681466, 4.060342411631854]

The 90% confidence interval $\ci{\Delta,0.9} = [1.94, 4.06]$ describes an interval of numbers that should contain the difference between group means $\Delta$ at least 90% of the time:

\[ \textrm{Pr}_{\mathbf{X}}\big(\{ \Delta \in \ci{\Delta,0.9} \}\big) \geq 0.9. \]

Reusable procedure for two-sample $t$-test#

#######################################################

def ttest_dmeans(xsample, ysample):
    # Calculate the observed difference between means
    obsdhat = mean(xsample) - mean(ysample)

    # Calculate the sample sizes and the stds
    n, m = len(xsample), len(ysample)
    sx, sy = std(xsample), std(ysample)

    # Calculate the standard error, the degrees of
    # freedom, the null model, and the t-statistic
    seD = np.sqrt(sx**2/n + sy**2/m)
    dfD = calcdf(sx, n, sy, m)
    obst = (obsdhat - 0) / seD

    # Calculate the p-value from the t-distribution
    rvT0 = tdist(df=dfD)
    pvalue = tailprobs(rvT0, obst, alt="two-sided")
    return pvalue

Verify we get the same $p$-value when using the standard error formula.

ttest_dmeans(pricesW, pricesE)

0.00025703383372176864

Example 6T: comparing rural and urban sleep scores#

students = pd.read_csv("../datasets/students.csv")
# students
# students.groupby("curriculum")["score"].describe()

scoresD = students[students["curriculum"]=="debate"]["score"]
scoresL = students[students["curriculum"]=="lecture"]["score"]

# observed difference between score means
dscores = dmeans(scoresD, scoresL)
dscores

8.319642857142853

ttest_dmeans(scoresD, scoresL)

0.10307495448387446

# FIGURES ONLY
filename = os.path.join(DESTDIR, "rvT0_p-value_dmeans_student_scores.pdf")

# T-TEST ANALYSIS
nD, nL = len(scoresD), len(scoresL)
stdD, stdL = std(scoresD), std(scoresL)
seDDL = np.sqrt(stdD**2/nD + stdL**2/nL)

obstDL = (dscores - 0) / seDDL

from ministats import calcdf
dfDL = calcdf(stdD, nD, stdL, nL)
rvT0DL = tdist(df=dfDL)
pvalueDL = tailprobs(rvT0DL, obstDL, alt="two-sided")
print(pvalueDL)

from ministats import calc_prob_and_plot_tails
_, ax = calc_prob_and_plot_tails(rvT0DL, -obstDL, obstDL, xlims=[-4,4])
ax.set_title(None)
ax.set_xlabel("$t$")
ax.set_ylabel("$f_{T_0}$")

savefigure(ax, filename)

0.10307495448387446

Saved figure to figures/stats/two_sample_tests/rvT0_p-value_dmeans_student_scores.pdf
Saved figure to figures/stats/two_sample_tests/rvT0_p-value_dmeans_student_scores.png

../_images/b79bb2e4cb0aed2296c5f37f83e05802b149bdaaebafd2e1cda2da7477074bb6.png

Alternative calculation methods#

Two-sample $t$-test using pooled variance#

Pooled variance formulas#

Example 5T revisited with pooled variance#

# TODO make self contained

# Compute the pooled variance and standard error of estimator D
varp = ((nW-1)*stdW**2 + (nE-1)*stdE**2) / (nW + nE - 2)
stdp = np.sqrt(varp)
seDp = stdp * np.sqrt(1/nW + 1/nE)
seDp

0.5972674401486561

# Compute the value of the t-statistic
obstp = (dprice - 0) / seDp
obstp

5.022875513276463

# Obtain the degrees of freedom
dfDp = nW + nW - 2
dfDp

from scipy.stats import t as tdist
from ministats import tailprobs

# Calculate the p-value
rvT0p = tdist(df=dfDp)
pvaluep = tailprobs(rvT0p, obstp, alt="two-sided")
pvaluep

0.00012497067987674894

Using `scipy.stats.ttest_ind` for two-sample $t$-tests#

Alternatively, we can use scipy.stats.ttest_ind to obtain the $p$-value.

Use equal_var=False to obtain the Welsh value.

# ALT. compute using existing function in `scipy.stats`
from scipy.stats import ttest_ind
res1 = ttest_ind(pricesW, pricesE, equal_var=False)
res1.pvalue

0.0002570338337217609

Use equal_var=True to obtain the pooled variance value.

# ALT. compute using existing function in `scipy.stats`
from scipy.stats import ttest_ind
res2 = ttest_ind(pricesW, pricesE, equal_var=True)
res2.pvalue

0.00012497067987678488

Using `scipy.stats.ttest_ind` for permutation test#

You can use the SciPy implementation of permutation test, by calling ttest_ind(..., permutations=10000) to perform a permutation test, then obtain the $p$-value.

from scipy.stats import ttest_ind

np.random.seed(42)
ttest_ind(pricesW, pricesE, permutations=10000).pvalue

0.00029997000299970003

Note the $p$-value we obtained form the two methods may be different. This can happen when using the permutations test, because we use randomness as part of the calculation.

Using `statsmodels` for two-sample $t$-tests#

import statsmodels.stats.api as sms

statsW = sms.DescrStatsW(pricesW)
statsE = sms.DescrStatsW(pricesE)
cm = sms.CompareMeans(statsW, statsE)

# Welch's t-test
cm.ttest_ind(alternative="two-sided", usevar="unequal")

(5.022875513276463, 0.000257033833721762, 12.592817027231028)

# T-test with pooled variance
cm.ttest_ind(alternative="two-sided", usevar="pooled")

(5.022875513276463, 0.00012497067987678534, 16.0)

Explanations#

Statistical modelling assumptions#

INDEP:
NORMAL:
LARGEn:
EQVAR:

Standardized effect size#

It is sometimes useful to report the effect size using a “standardized” measure for effect sizes.

Cohen’s $d$ is one such measure, and it is defined as the difference between two means divided by the pooled standard deviation.

\[ d = \frac{\overline{\mathbf{x}} - \overline{\mathbf{y}} }{ s_{p} }. \]

where the pooled variance is defined as $s_{p}^2 = [(n -1)s_{\mathbf{x}}^2 + (m -1)s_{\mathbf{y}}^2]/(n + m -2)$.

def cohend2(sample1, sample2):
    """
    Cohen's d measure of effect size for two independent samples.
    """
    n1, n2 = len(sample1), len(sample2)
    mean1, mean2 = mean(sample1), mean(sample2)
    var1, var2 = var(sample1), var(sample2)
    # calculate the pooled variance and std
    var_pooled = ((n1-1)*var1+(n2-1)*var2) / (n1+n2-2)
    std_pooled = np.sqrt(var_pooled)
    d = (mean1 - mean2) / std_pooled
    return d

We interpret the value of Cohen’s $d$ using the reference table of values:

Cohen’s d	Effect size
0.01	very small
0.20	small
0.50	medium
0.80	large

Effect size for mean deviation of kombucha Batch 04 from expected value $\mu_K=1000$.

cohend2(pricesW, pricesE)

2.3678062243290983

Discussion#

Comparison to resampling methods#

Exercises#

See notebook exercises_35_two_sample_tests.ipynb.

Links#

Permutation Methods: A Basis for Exact Inference by Michael D. Ernst
Nice animation https://commons.wikimedia.org/wiki/File:Permutation_test_example_animation.gif
via https://en.wikipedia.org/wiki/Permutation_test

Section 3.5 — Two-sample hypothesis tests

Contents

Section 3.5 — Two-sample hypothesis tests#

Notebook setup#

Definitions#

Comparing two groups#

Computing \(p\)-values#

Permutation test for comparing two populations#

Permutations#

Resampling under the null hypothesis#

Example 5P: electricity prices#

Running a permutation test#

Effect size estimates#

Reusable function#

Example 6P: lecture and debate curriculums#

Analytical approximation methods#

Example 5T: comparing East and West electricity prices#

Two-sample t-test#

Effect size estimates#

Reusable procedure for two-sample \(t\)-test#

Example 6T: comparing rural and urban sleep scores#

Alternative calculation methods#

Two-sample \(t\)-test using pooled variance#

Pooled variance formulas#

Example 5T revisited with pooled variance#

Using `scipy.stats.ttest_ind` for two-sample \(t\)-tests#

Using `scipy.stats.ttest_ind` for permutation test#

Using `statsmodels` for two-sample \(t\)-tests#

Explanations#

Statistical modelling assumptions#

Standardized effect size#

Discussion#

Comparison to resampling methods#

Exercises#

Links#

Section 3.5 — Two-sample hypothesis tests

Contents

Section 3.5 — Two-sample hypothesis tests#

Notebook setup#

Definitions#

Comparing two groups#

Computing \(p\)-values#

Permutation test for comparing two populations#

Permutations#

Resampling under the null hypothesis#

Example 5P: electricity prices#

Running a permutation test#

Effect size estimates#

Reusable function#

Example 6P: lecture and debate curriculums#

Analytical approximation methods#

Example 5T: comparing East and West electricity prices#

Two-sample t-test#

Effect size estimates#

Reusable procedure for two-sample \(t\)-test#

Example 6T: comparing rural and urban sleep scores#

Alternative calculation methods#

Two-sample \(t\)-test using pooled variance#

Pooled variance formulas#

Example 5T revisited with pooled variance#

Using scipy.stats.ttest_ind for two-sample \(t\)-tests#

Using scipy.stats.ttest_ind for permutation test#

Using statsmodels for two-sample \(t\)-tests#

Explanations#

Statistical modelling assumptions#

Standardized effect size#

Discussion#

Comparison to resampling methods#

Exercises#

Links#

Using `scipy.stats.ttest_ind` for two-sample \(t\)-tests#

Using `scipy.stats.ttest_ind` for permutation test#

Using `statsmodels` for two-sample \(t\)-tests#