Section 5.5 — Hierarchical models

Section 5.5 — Hierarchical models#

This notebook contains the code examples from Section 5.5 Hierarchical models from the No Bullshit Guide to Statistics.

See also:

Notebook setup#

# Ensure required Python modules are installed
# %pip install --quiet numpy scipy seaborn statsmodels bambi==0.15.0 pymc==5.23.0 ministats

# Load Python modules
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Figures setup
plt.clf()  # needed otherwise `sns.set_theme` doesn't work
sns.set_theme(
    context="paper",
    style="whitegrid",
    palette="colorblind",
    rc={"font.family": "serif",
        "font.serif": ["Palatino", "DejaVu Serif", "serif"],
        "figure.figsize": (5,3)},
)
%config InlineBackend.figure_format = "retina"

<Figure size 640x480 with 0 Axes>

# Simple float __repr__  
if int(np.__version__.split(".")[0]) >= 2:
    np.set_printoptions(legacy='1.25')

# Set random seed for repeatability
np.random.seed(42)

# Download datasets/ directory if necessary
from ministats import ensure_datasets
ensure_datasets()

datasets/ directory already exists.

# silence statsmodels kurtosistest warning when using n < 20
import warnings
warnings.filterwarnings("ignore", category=FutureWarning)
warnings.filterwarnings("ignore", category=UserWarning)

# silence ERROR messages when showing model graphs
# cf. https://github.com/pymc-devs/pymc/issues/7901
import logging
logging.getLogger("pytensor.graph.rewriting.basic").setLevel(logging.CRITICAL)

Definitions#

Hierarchical (multilevel) models#

Model formula#

A Bayesian hierarchical model is described by the following equations:

\(\def\calN{\mathcal{N}} \def\Tdist{\mathcal{T}} \def\Expon{\mathrm{Expon}}\)

\[\begin{align*} X_j &\sim \calN(M_{j}, \, \Sigma_X), \\ M_{j} &= B_0 + B_{0j}, \\ \Sigma_X &\sim \Tdist^+\!(\nu_{\Sigma_X}, \sigma_{\Sigma_X}), \\ B_0 &\sim \calN(\mu_{B_0},\sigma_{B_0}), \\ B_{0j} &\sim \calN(0,\Sigma_{B_{0j}}), \\ \Sigma_{B_{0j}} &\sim \Expon(\lambda). \end{align*}\]

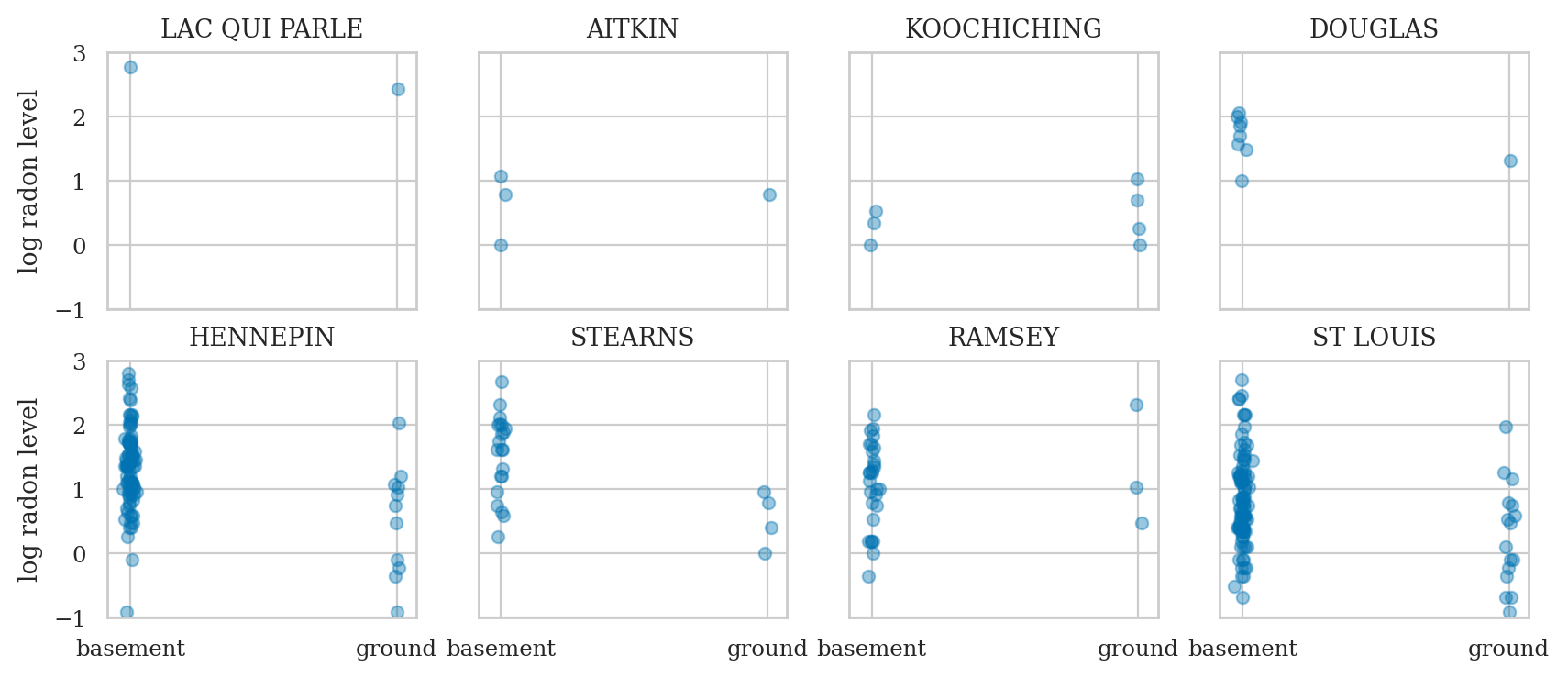
Radon dataset#

https://bambinos.github.io/bambi/notebooks/radon_example.html

  • Description: Contains measurements of radon levels in homes across various counties.

  • Source: Featured in Andrew Gelman and Jennifer Hill’s book Data Analysis Using Regression and Multilevel/Hierarchical Models.

  • Application: Demonstrates partial pooling and varying intercepts/slopes in hierarchical modeling.

Loading the data#

radon = pd.read_csv("datasets/radon.csv")
radon.shape

(919, 6)

radon.head()
idnum state county floor log_radon log_uranium
0 5081 MN AITKIN ground 0.788457 -0.689048
1 5082 MN AITKIN basement 0.788457 -0.689048
2 5083 MN AITKIN basement 1.064711 -0.689048
3 5084 MN AITKIN basement 0.000000 -0.689048
4 5085 MN ANOKA basement 1.131402 -0.847313

Descriptive statistics#

radon["log_radon"].describe()

count    919.000000
mean       1.224623
std        0.853327
min       -2.302585
25%        0.641854
50%        1.280934
75%        1.791759
max        3.875359
Name: log_radon, dtype: float64

len(radon["county"].unique())

85

radon["floor"].value_counts()

floor
basement    766
ground      153
Name: count, dtype: int64

from ministats.book.figures import plot_counties
sel_counties = [
  "LAC QUI PARLE", "AITKIN", "KOOCHICHING", "DOUGLAS",
  "HENNEPIN", "STEARNS", "RAMSEY", "ST LOUIS",
]
plot_counties(radon, counties=sel_counties);
../_images/1daf076aa94e30418f63022f16449bdc157fa918cd768bac2d06fd50a708464f.png

Example 1: complete pooling model#

= common linear regression model for all counties

Bayesian model#

We can pool all the data and estimate one big regression to asses the influence of the floor variable on radon levels across all counties.

\[\begin{align*} R &\sim \calN(M_R, \, \Sigma_R), \\ M_R &= B_0 + B_{\!f}\!\cdot\!f, \\ \Sigma_R &\sim \Tdist^+\!(4, 1), \\ B_0 &\sim \calN(1, 2), \\ B_f &\sim \calN(0, 5). \end{align*}\]

The variable \(f\) corresponds to the column floor in the radon data frame, which will be internally coded as binary with \(0\) representing basement, and \(1\) representing ground floor.

By ignoring the county feature, we do not differenciate on counties.

Bambi model#

import bambi as bmb

priors1 = {
    "Intercept": bmb.Prior("Normal", mu=1, sigma=2),
    "floor": bmb.Prior("Normal", mu=0, sigma=5),
    "sigma": bmb.Prior("HalfStudentT", nu=4, sigma=1),
}

mod1 = bmb.Model(formula="log_radon ~ 1 + floor",
                 family="gaussian",
                 link="identity",
                 priors=priors1,
                 data=radon)
mod1

       Formula: log_radon ~ 1 + floor
        Family: gaussian
          Link: mu = identity
  Observations: 919
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 1.0, sigma: 2.0)
            floor ~ Normal(mu: 0.0, sigma: 5.0)
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 1.0)

mod1.build()
mod1.graph()
../_images/6981f2fb5f90e62e447f5f0d2e73b4e9e9ea364890cb2489b5e1990a2375ca9f.svg

Model fitting and analysis#

idata1 = mod1.fit(random_seed=42)

Initializing NUTS using jitter+adapt_diag...

Multiprocess sampling (2 chains in 2 jobs)

NUTS: [sigma, Intercept, floor]



Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 1 seconds.





We recommend running at least 4 chains for robust computation of convergence diagnostics













import arviz as az

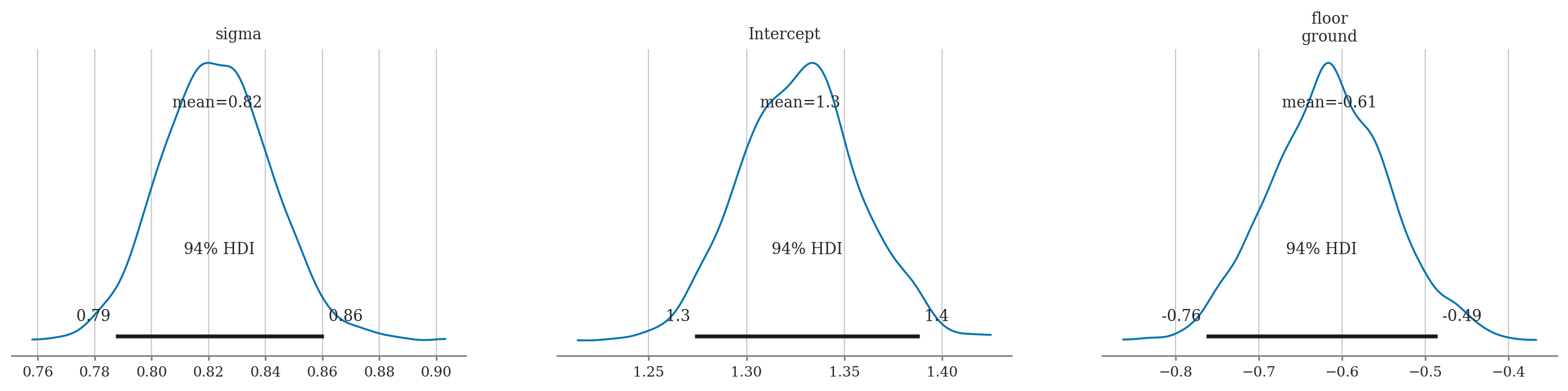
az.summary(idata1, kind="stats")













  
    

      
      mean
      sd
      hdi_3%
      hdi_97%
    

  
  
    

      sigma
      0.823
      0.020
      0.787
      0.860
    

    

      Intercept
      1.327
      0.031
      1.274
      1.389
    

    

      floor[ground]
      -0.615
      0.073
      -0.763
      -0.485
    

  











az.plot_posterior(idata1);








../_images/c569d5ea072a4d80dfccc0f5f0b53639db15a6240d16e326b1d55b893c441039.png










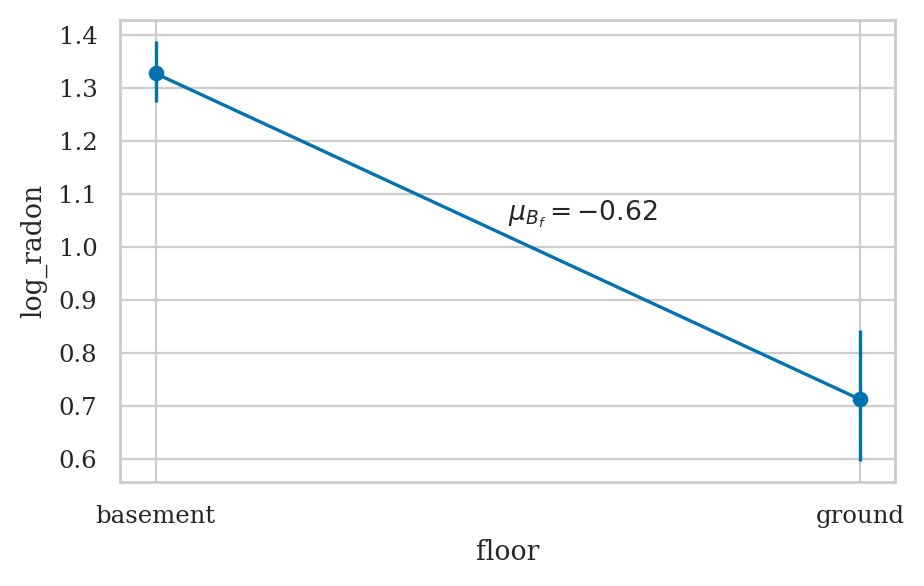
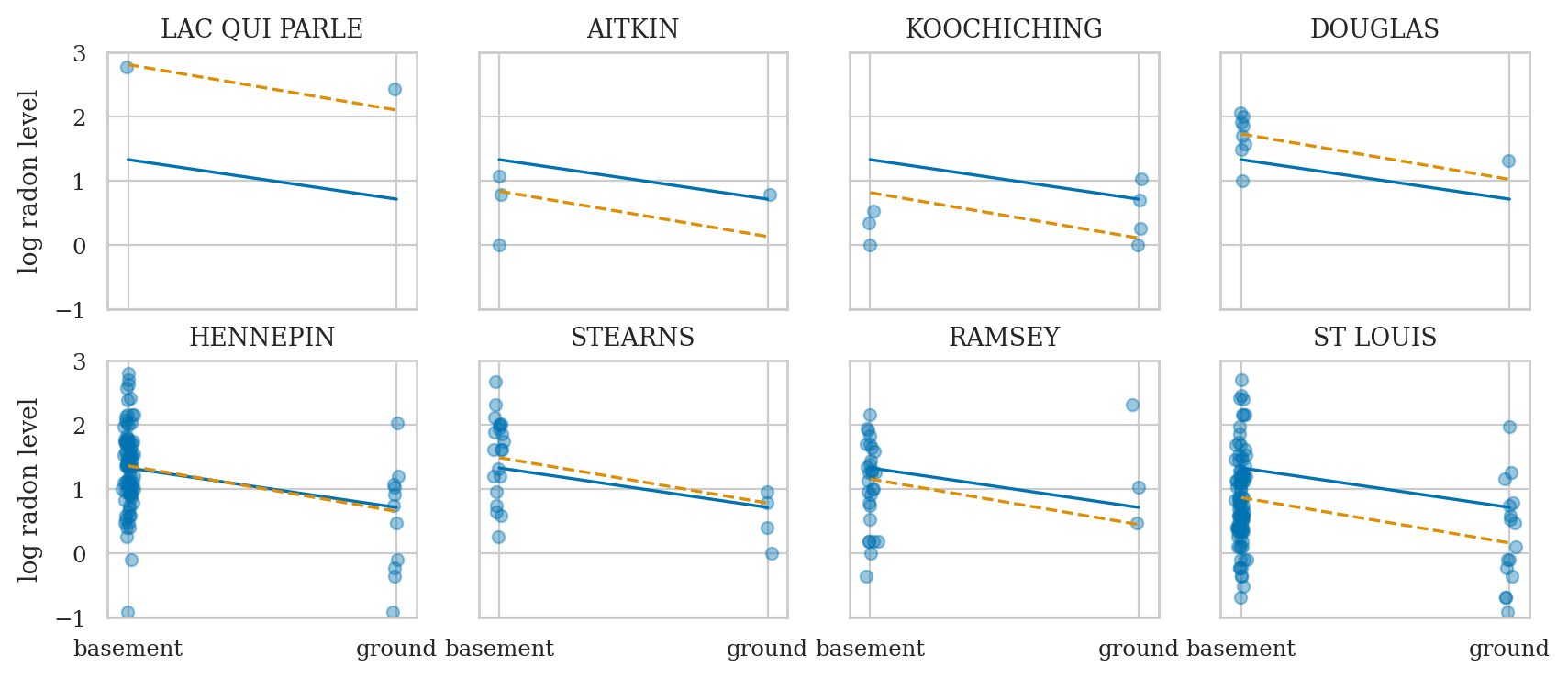
fig, axs = bmb.interpret.plot_predictions(mod1, idata1, conditional="floor")

means1 = az.summary(idata1, kind="stats")["mean"]
y0 = means1["Intercept"]
y1 = means1["Intercept"] + means1["floor[ground]"]
sns.lineplot(x=[0,1], y=[y0,y1], ax=axs[0]);

midpoint = [0.5, (y0+y1)/2 + 0.03]
slope = means1["floor[ground]"].round(2)
axs[0].annotate("$\\mu_{B_{f}}=%.2f$" % slope, midpoint);









Default computed for conditional variable: floor




../_images/50f2ddd5cafa8d5d502548df5fdfb30b23e43ba4f6dd6b981e85f19cd4d6bee8.png










Conclusion#


not using group membership, so we have lots of bias








Example 2: no pooling model#


= separate intercept for each county




Bayesian model#


If we treat different counties as independent,
so each one gets an intercept term:



\[\begin{align*}
    R_j			&\sim	\calN(M_j, \, \Sigma_R),  					\\
    M_j			&=		B_{0j} + B_{\!f}\!\cdot\!f,					\\
    \Sigma_R		&\sim	\Tdist^+\!(4, 1),							\\
    B_{0j}		&\sim	\calN(1, 2),							\\
    B_f			&\sim	\calN(0, 5).
\end{align*}\]






Bambi model#






priors2 = {
    "county": bmb.Prior("Normal", mu=1, sigma=2),
    "floor": bmb.Prior("Normal", mu=0, sigma=5),
    "sigma": bmb.Prior("HalfStudentT", nu=4, sigma=1),
}

mod2 = bmb.Model("log_radon ~ 0 + county + floor",
                 family="gaussian",
                 link="identity",
                 priors=priors2,
                 data=radon)
mod2









       Formula: log_radon ~ 0 + county + floor
        Family: gaussian
          Link: mu = identity
  Observations: 919
        Priors: 
    target = mu
        Common-level effects
            county ~ Normal(mu: 1.0, sigma: 2.0)
            floor ~ Normal(mu: 0.0, sigma: 5.0)
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 1.0)













mod2.build()
mod2.graph()








../_images/95f456bb2f0bec47965d4ef989a591f6123adf04ffa2a26927afd1feb542d6fc.svg









Model fitting and analysis#






idata2 = mod2.fit(random_seed=42)









Initializing NUTS using jitter+adapt_diag...





Multiprocess sampling (2 chains in 2 jobs)





NUTS: [sigma, county, floor]







Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 4 seconds.





We recommend running at least 4 chains for robust computation of convergence diagnostics





The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details













idata2sel = idata2.sel(county_dim=sel_counties)
az.summary(idata2sel, kind="stats")













  
    

      
      mean
      sd
      hdi_3%
      hdi_97%
    

  
  
    

      sigma
      0.756
      0.019
      0.719
      0.790
    

    

      county[LAC QUI PARLE]
      2.807
      0.529
      1.769
      3.760
    

    

      county[AITKIN]
      0.837
      0.373
      0.149
      1.558
    

    

      county[KOOCHICHING]
      0.814
      0.292
      0.232
      1.341
    

    

      county[DOUGLAS]
      1.728
      0.251
      1.233
      2.164
    

    

      county[HENNEPIN]
      1.359
      0.077
      1.220
      1.504
    

    

      county[STEARNS]
      1.488
      0.152
      1.221
      1.776
    

    

      county[RAMSEY]
      1.154
      0.136
      0.883
      1.393
    

    

      county[ST LOUIS]
      0.866
      0.073
      0.723
      1.000
    

    

      floor[ground]
      -0.707
      0.073
      -0.838
      -0.564
    

  











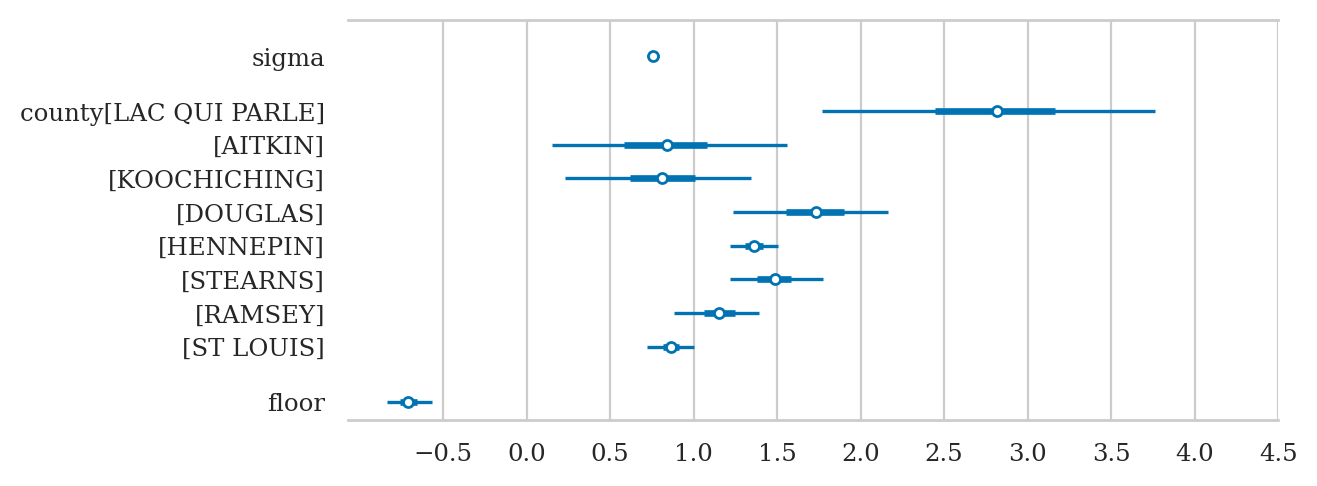
axs = az.plot_forest(idata2sel, combined=True, figsize=(6,2.6))
axs[0].set_xticks(np.arange(-0.5,4.6,0.5))
axs[0].set_title(None);








../_images/85d417f04ef4e67a4bd71a64628506a60bdc57b95817ed0bfb0197212626b997.png










plot_counties(radon, idata_cp=idata1, idata_np=idata2);








../_images/846c375e8dc1b7565b4cc701ff0a038224e34d9daa1e5afc7c301db7806e04da.png










# fig, axs = bmb.interpret.plot_predictions(mod2, idata2, ["floor", "county"]);
# axs[0].get_legend().remove()













# post2 = idata2["posterior"]
# unpooled_means = post2.mean(dim=("chain", "draw"))
# unpooled_hdi = az.hdi(idata2)

# unpooled_means_iter = unpooled_means.sortby("county")
# unpooled_hdi_iter = unpooled_hdi.sortby(unpooled_means_iter.county)

# _, ax = plt.subplots(figsize=(12, 5))
# unpooled_means_iter.plot.scatter(x="county_dim", y="county", ax=ax, alpha=0.9)
# ax.vlines(
#     np.arange(len(radon["county"].unique())),
#     unpooled_hdi_iter.county.sel(hdi="lower"),
#     unpooled_hdi_iter.county.sel(hdi="higher"),
#     color="orange",
#     alpha=0.6,
# )
# ax.set(ylabel="Radon estimate", ylim=(-2, 4.5))
# ax.tick_params(rotation=90);













Conclusion#


treating each group independently, so we have lots of variance






# TODO:
# calculate the std.dev. of the county-specific slopes -- this is like \Sigma_J but w/o a prior.















Example 3: hierarchical model#


= partial pooling model
= varying intercepts model




Bayesian hierarchical model#



\[\begin{align*}
    R_j			&\sim	\calN(M_j, \, \Sigma_R),						\\
    M_j			&=		B_0 + B_{0j} + B_f\!\cdot\!f,					\\
    \Sigma_R	&\sim	\Tdist^+\!(4, 1),								\\
    B_0			&\sim	\calN(1,2),										\\
    B_{0j}		&\sim	\calN(0,\Sigma_{B_{0j}}),						\\
    B_f			&\sim	\calN(0, 5),									\\
    \Sigma_{B_{0j}}	&\sim	\Expon(1).
\end{align*}\]


The partial pooling formula estimates per-county intercepts which drawn
from the same distribution which is estimated jointly with the rest of
the model parameters. The 1 is the intercept co-efficient. The
estimates across counties will all have the same slope.


log_radon ~ 1 + (1|county_id) + floor





There is a middle ground to both of these extremes.
Specifically, we may assume that the intercepts are different for each county as in the unpooled case,
but they are drawn from the same distribution.
The different counties are effectively sharing information through the common prior.


NOTE: some counties have very few sample; the hierarchical model will provide “shrinkage” for these groups, and use global information learned from all counties






radon["log_radon"].describe()









count    919.000000
mean       1.224623
std        0.853327
min       -2.302585
25%        0.641854
50%        1.280934
75%        1.791759
max        3.875359
Name: log_radon, dtype: float64













radon.groupby("floor")["log_radon"].describe()













  
    

      
      count
      mean
      std
      min
      25%
      50%
      75%
      max
    

    

      floor
      
      
      
      
      
      
      
      
    

  
  
    

      basement
      766.0
      1.326744
      0.782709
      -2.302585
      0.788457
      1.360977
      1.883253
      3.875359
    

    

      ground
      153.0
      0.713349
      0.999376
      -2.302585
      0.095310
      0.741937
      1.308333
      3.234749
    

  











Bambi model#






priors3 = {
    "Intercept": bmb.Prior("Normal", mu=1, sigma=2),
    "floor": bmb.Prior("Normal", mu=0, sigma=5),
    "1|county": bmb.Prior("Normal", mu=0, sigma=bmb.Prior("Exponential", lam=1)),
    "sigma": bmb.Prior("HalfStudentT", nu=4, sigma=1),
}

formula3 = "log_radon ~ 1 + (1|county) + floor"
mod3 = bmb.Model(formula=formula3,
                 family="gaussian",
                 link="identity",
                 priors=priors3,
                 data=radon,
                 noncentered=False)

mod3









       Formula: log_radon ~ 1 + (1|county) + floor
        Family: gaussian
          Link: mu = identity
  Observations: 919
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 1.0, sigma: 2.0)
            floor ~ Normal(mu: 0.0, sigma: 5.0)
        
        Group-level effects
            1|county ~ Normal(mu: 0.0, sigma: Exponential(lam: 1.0))
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 1.0)













mod3.build()
mod3.graph()








../_images/ca579e767a5aba08ca3e62d712d80f3f6253af43305fbeecb22ab2b53e6484fc.svg









Model fitting and analysis#






idata3 = mod3.fit(random_seed=42)









Initializing NUTS using jitter+adapt_diag...





Multiprocess sampling (2 chains in 2 jobs)





NUTS: [sigma, Intercept, floor, 1|county_sigma, 1|county]







Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 3 seconds.





We recommend running at least 4 chains for robust computation of convergence diagnostics









The group level parameters






idata3sel = idata3.sel(county__factor_dim=sel_counties)
az.summary(idata3sel, kind="stats")













  
    

      
      mean
      sd
      hdi_3%
      hdi_97%
    

  
  
    

      sigma
      0.757
      0.019
      0.724
      0.792
    

    

      Intercept
      1.457
      0.052
      1.357
      1.549
    

    

      floor[ground]
      -0.693
      0.071
      -0.824
      -0.561
    

    

      1|county_sigma
      0.332
      0.046
      0.250
      0.421
    

    

      1|county[LAC QUI PARLE]
      0.418
      0.295
      -0.136
      0.973
    

    

      1|county[AITKIN]
      -0.269
      0.261
      -0.761
      0.210
    

    

      1|county[KOOCHICHING]
      -0.368
      0.224
      -0.797
      0.044
    

    

      1|county[DOUGLAS]
      0.170
      0.200
      -0.193
      0.543
    

    

      1|county[HENNEPIN]
      -0.092
      0.089
      -0.263
      0.062
    

    

      1|county[STEARNS]
      0.020
      0.138
      -0.255
      0.265
    

    

      1|county[RAMSEY]
      -0.257
      0.135
      -0.510
      -0.005
    

    

      1|county[ST LOUIS]
      -0.565
      0.086
      -0.716
      -0.397
    

  







The intercept offsets for each county are:






# sum( idata3["posterior"]["1|county"].stack(sample=("chain","draw")).values.mean(axis=1) )













# az.plot_forest(idata3, combined=True, figsize=(7,2),
#                var_names=["Intercept", "floor", "1|county_sigma", "sigma"]);













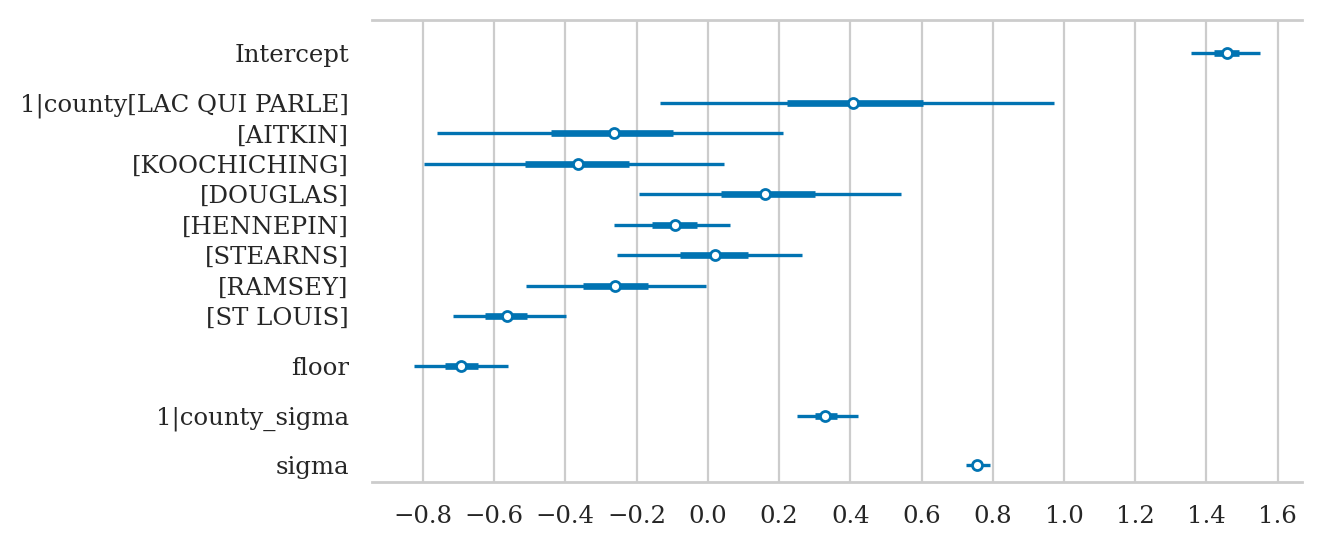
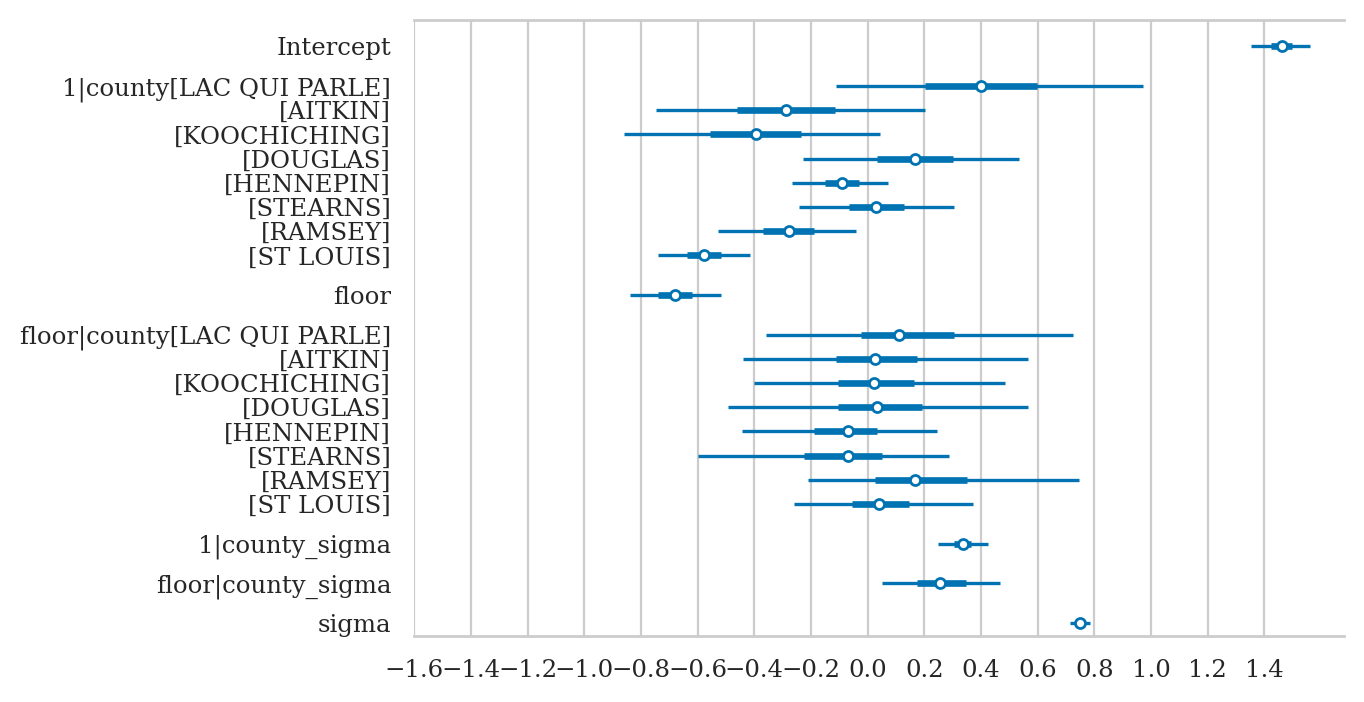
axs = az.plot_forest(idata3sel,
                     var_names=["Intercept", "1|county", "floor", "1|county_sigma", "sigma"],
                     combined=True, figsize=(6,3))
axs[0].set_xticks(np.arange(-0.8,1.6,0.2))
axs[0].set_title(None);








../_images/d8375404a97ba43d9d5bbac956641dc5ae1ab760f8b692799cffc3fcee99a127.png










# az.plot_forest(idata3, var_names=["1|county"], combined=True);













Compare models#


Compare complete pooling,  no pooling, and partial pooling models






plot_counties(radon, idata_cp=idata1, idata_np=idata2, idata_pp=idata3);








../_images/eb0ef466096e0e11a1881340eff71f6c77ce31ba4dcd8248880e788b84f6a0b3.png










# # Forest plot comparing `mod2` and `mod3` estimates
# # (to illustrate reduced uncertainty in estimates + shrinkage)
# post3 = idata3sel["posterior"]
# post3["county"] = post3["Intercept"] + post3["1|county"]
# axs = az.plot_forest([idata2sel, idata3sel], model_names=["mod2", "mod3"],
#                      var_names=["county", "floor", "1|county_sigma", "sigma"], combined=True, figsize=(6,3))
# ax = axs[0]
# rbar = radon["log_radon"].mean()
# ax.axvline(rbar, ls="--");













Conclusions#








Explanations#




Prior selection for hierarchical models#


?






Varying intercepts and slopes model#


= Group-specific slopes
We can also make beta_x group-specific


The varying-slope, varying intercept model adds floor to the
group-level co-efficients. Now estimates across counties will all have
varying slope.


log_radon ~ 1 + floor + (1 + floor | county)









#######################################################
formula4 = "log_radon ~ 1 + (1|county) + floor + (floor|county)"

SigmaB0j = bmb.Prior("Exponential", lam=1)
SigmaBfj = bmb.Prior("Exponential", lam=1)

priors4 = {
    "Intercept": bmb.Prior("Normal", mu=1, sigma=2),
    "1|county": bmb.Prior("Normal", mu=0, sigma=SigmaB0j),
    "floor": bmb.Prior("Normal", mu=-1, sigma=2),
    "floor|county": bmb.Prior("Normal", mu=0, sigma=SigmaBfj),
    "sigma": bmb.Prior("HalfStudentT", nu=4, sigma=1),
}

mod4 = bmb.Model(formula=formula4,
                 family="gaussian",
                 link="identity",
                 priors=priors4,
                 data=radon,
                 noncentered=False)
mod4









       Formula: log_radon ~ 1 + (1|county) + floor + (floor|county)
        Family: gaussian
          Link: mu = identity
  Observations: 919
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 1.0, sigma: 2.0)
            floor ~ Normal(mu: -1.0, sigma: 2.0)
        
        Group-level effects
            1|county ~ Normal(mu: 0.0, sigma: Exponential(lam: 1.0))
            floor|county ~ Normal(mu: 0.0, sigma: Exponential(lam: 1.0))
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 1.0)













mod4.build()
mod4.graph()








../_images/af9ec1b03e28f528c0e2431151b79ed9180f7df031ca5b63165fc876b5fcc1d7.svg









idata4 = mod4.fit(draws=2000, tune=3000, random_seed=42, target_accept=0.9)









Initializing NUTS using jitter+adapt_diag...





Multiprocess sampling (2 chains in 2 jobs)





NUTS: [sigma, Intercept, floor, 1|county_sigma, 1|county, floor|county_sigma, floor|county]







Sampling 2 chains for 3_000 tune and 2_000 draw iterations (6_000 + 4_000 draws total) took 16 seconds.





We recommend running at least 4 chains for robust computation of convergence diagnostics





The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details





The effective sample size per chain is smaller than 100 for some parameters.  A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details













# az.autocorr(idata4["posterior"]["sigma"].values.flatten())[0:10]













idata4sel = idata4.sel(county__factor_dim=sel_counties)
az.summary(idata4sel, kind="stats")













  
    

      
      mean
      sd
      hdi_3%
      hdi_97%
    

  
  
    

      sigma
      0.750
      0.019
      0.714
      0.784
    

    

      Intercept
      1.461
      0.055
      1.352
      1.561
    

    

      floor[ground]
      -0.679
      0.086
      -0.838
      -0.516
    

    

      1|county_sigma
      0.338
      0.047
      0.249
      0.425
    

    

      1|county[LAC QUI PARLE]
      0.403
      0.293
      -0.110
      0.970
    

    

      1|county[AITKIN]
      -0.289
      0.253
      -0.746
      0.203
    

    

      1|county[KOOCHICHING]
      -0.397
      0.239
      -0.862
      0.043
    

    

      1|county[DOUGLAS]
      0.168
      0.202
      -0.229
      0.534
    

    

      1|county[HENNEPIN]
      -0.091
      0.090
      -0.266
      0.071
    

    

      1|county[STEARNS]
      0.032
      0.145
      -0.242
      0.304
    

    

      1|county[RAMSEY]
      -0.279
      0.132
      -0.528
      -0.040
    

    

      1|county[ST LOUIS]
      -0.577
      0.087
      -0.740
      -0.415
    

    

      floor|county_sigma[ground]
      0.266
      0.120
      0.051
      0.467
    

    

      floor|county[ground, LAC QUI PARLE]
      0.155
      0.285
      -0.358
      0.725
    

    

      floor|county[ground, AITKIN]
      0.037
      0.258
      -0.440
      0.567
    

    

      floor|county[ground, KOOCHICHING]
      0.032
      0.228
      -0.399
      0.485
    

    

      floor|county[ground, DOUGLAS]
      0.048
      0.268
      -0.491
      0.567
    

    

      floor|county[ground, HENNEPIN]
      -0.082
      0.181
      -0.445
      0.246
    

    

      floor|county[ground, STEARNS]
      -0.093
      0.227
      -0.599
      0.286
    

    

      floor|county[ground, RAMSEY]
      0.209
      0.262
      -0.210
      0.744
    

    

      floor|county[ground, ST LOUIS]
      0.045
      0.163
      -0.259
      0.370
    

  











az.summary(idata4, var_names="sigma", kind="stats")













  
    

      
      mean
      sd
      hdi_3%
      hdi_97%
    

  
  
    

      sigma
      0.75
      0.019
      0.714
      0.784
    

  







The estimated mean standard deviation is the lowest of all the models we considered so far.






plot_counties(radon, idata_cp=idata1, idata_np=idata2, idata_pp=idata3, idata_pp2=idata4);








../_images/48ef85c8e764457f3d98325c7768d8d5c8e13de79aea6e5e1cbff84131403d62.png










idata4sel = idata4.sel(county__factor_dim=sel_counties)
var_names = ["Intercept",
             "1|county",
             "floor",
             "floor|county",
             "1|county_sigma",
             "floor|county_sigma",
             "sigma"]
axs = az.plot_forest(idata4sel, combined=True, var_names=var_names, figsize=(6,4))
axs[0].set_xticks(np.arange(-1.6,1.6,0.2))
axs[0].set_title(None);








../_images/4582eff332eaef5c24c2ef5991ad3abb4af92095ff36270a6096a4b9eab6b248.png










Comparing models#






from ministats.utils import loglevel
with loglevel("ERROR", module="pymc"):
    idata1ll = mod1.fit(idata_kwargs={"log_likelihood": True}, random_seed=42, progressbar=False)
    idata2ll = mod2.fit(idata_kwargs={"log_likelihood": True}, random_seed=42, progressbar=False)
    idata3ll = mod3.fit(idata_kwargs={"log_likelihood": True}, random_seed=42, progressbar=False)
    idata4ll = mod4.fit(idata_kwargs={"log_likelihood": True}, random_seed=42, progressbar=False,
                        draws=2000, tune=3000, target_accept=0.9)









The effective sample size per chain is smaller than 100 for some parameters.  A higher number is needed for reliable rhat and ess computation. See https://arxiv.org/abs/1903.08008 for details









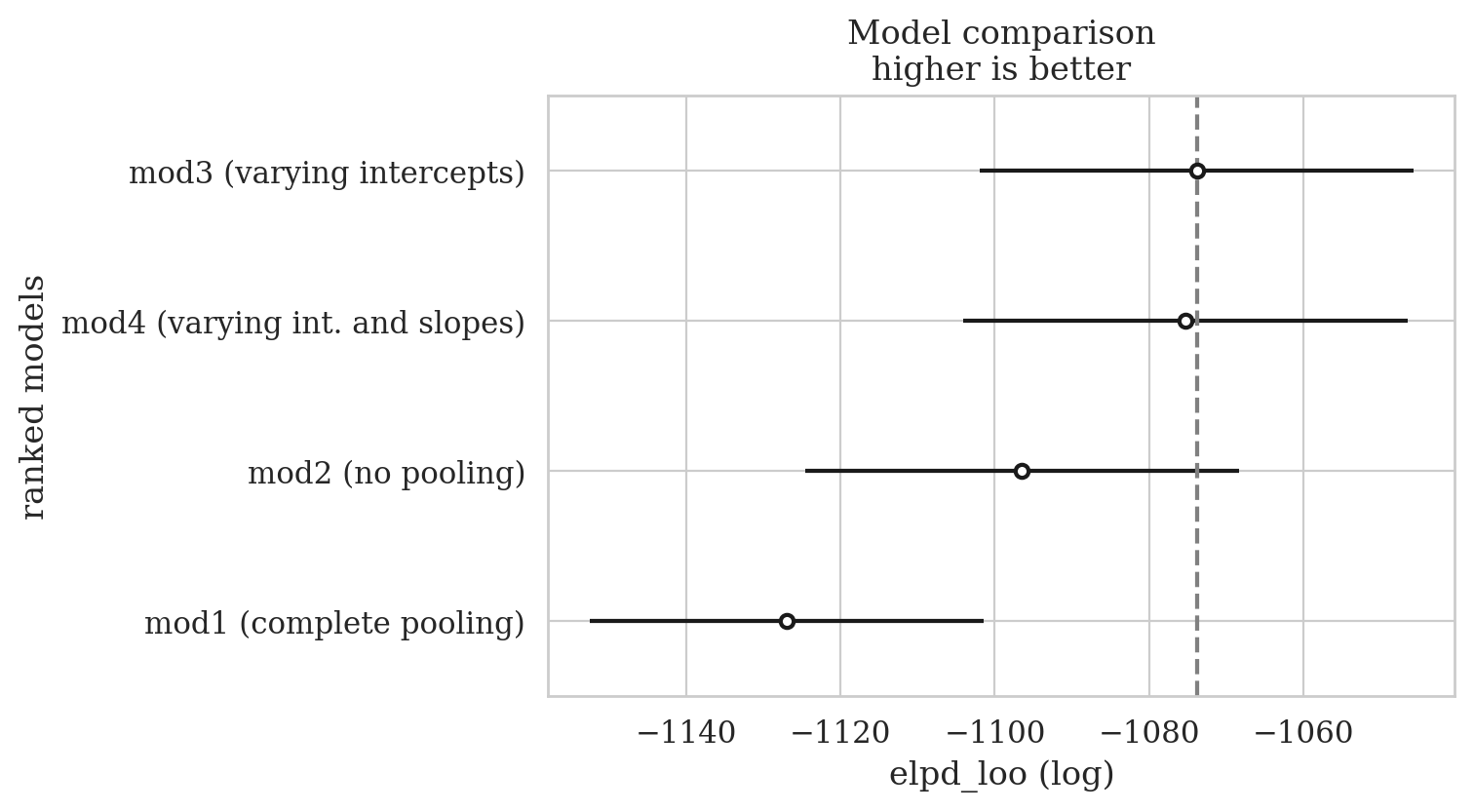
Compare models based on their expected log pointwise predictive density (ELPD).


The ELPD is estimated either by Pareto smoothed importance sampling leave-one-out cross-validation (LOO) or using the widely applicable information criterion (WAIC). We recommend loo. Read more theory here - in a paper by some of the leading authorities on model comparison dx.doi.org/10.1111/1467-9868.00353






radon_models = {
    "mod1 (complete pooling)": idata1ll,
    "mod2 (no pooling)": idata2ll,
    "mod3 (varying intercepts)": idata3ll,
    "mod4 (varying int. and slopes)": idata4ll,
}
compare_results = az.compare(radon_models)
compare_results













  
    

      
      rank
      elpd_loo
      p_loo
      elpd_diff
      weight
      se
      dse
      warning
      scale
    

  
  
    

      mod3 (varying intercepts)
      0
      -1073.808021
      48.948124
      0.000000
      0.498506
      28.106681
      0.000000
      True
      log
    

    

      mod4 (varying int. and slopes)
      1
      -1075.272478
      65.146294
      1.464458
      0.422125
      28.823094
      2.302895
      True
      log
    

    

      mod2 (no pooling)
      2
      -1096.474618
      83.787447
      22.666597
      0.000000
      28.092985
      6.110346
      True
      log
    

    

      mod1 (complete pooling)
      3
      -1126.982196
      3.833032
      53.174175
      0.079369
      25.565695
      10.579593
      False
      log
    

  











az.plot_compare(compare_results);








../_images/af3104546207ba3504d0df2ec9692467f463f5d0e1c50dc2783867c930a8ed0e.png








ELPD and elpd_loo#


The ELPD is the theoretical expected log pointwise predictive density for a new dataset (Eq 1 in VGG2017), which can be estimated, e.g., using cross-validation. elpd_loo is the Bayesian LOO estimate of the expected log pointwise predictive density (Eq 4 in VGG2017) and is a sum of N individual pointwise log predictive densities. Probability densities can be smaller or larger than 1, and thus log predictive densities can be negative or positive. For simplicity the ELPD acronym is used also for expected log pointwise predictive probabilities for discrete models. Probabilities are always equal or less than 1, and thus log predictive probabilities are 0 or negative.


via https://mc-stan.org/loo/reference/loo-glossary.html








Frequentist multilevel models#


We can use statsmodels to fit multilevel models too.




Random intercepts model using statsmodels#






import statsmodels.formula.api as smf
sm3 = smf.mixedlm("log_radon ~ 1 + floor",   # Fixed effects (no intercept and floor as a fixed effect)
                  groups="county",           # Grouping variable for random effects
                  re_formula="1",            # Random effects = intercept
                  data=radon)
res3 = sm3.fit()
res3.summary().tables[1]













  
    

      
      Coef.
      Std.Err.
      z
      P>|z|
      [0.025
      0.975]
    

  
  
    

      Intercept
      1.462
      0.052
      28.164
      0.000
      1.360
      1.563
    

    

      floor[T.ground]
      -0.693
      0.071
      -9.818
      0.000
      -0.831
      -0.555
    

    

      county Var
      0.108
      0.041
      
      
      
      
    

  











# slope
#######################################################
res3.params["floor[T.ground]"]









-0.692993740655805













# sigma-hat
np.sqrt(res3.scale)









0.7555891484188184













# standard deviation of the variability among county-specific Intercepts
np.sqrt(res3.cov_re)













  
    

      
      county
    

  
  
    

      county
      0.328222
    

  











# intercept deviation for first country in res3
res3.random_effects["LAC QUI PARLE"].values









array([0.40649212])













# compare with corresponding Bayesian point estimate
lqp = idata3.sel(county__factor_dim="LAC QUI PARLE")
post3_lqp_means = lqp["posterior"].mean()
post3_lqp_means["1|county"].values









array(0.41763279)









This is very close to the mean of the random effect coefficient for AITKIN in the Bayesian model mod3 which was \(-0.268\).






Random intercepts and slopes model using statsmodels (BONUS TOPIC)#






sm4 = smf.mixedlm("log_radon ~ 1 + floor",   # Fixed effects (no intercept and floor as a fixed effect)
                  groups="county",           # Grouping variable for random effects
                  re_formula="1 + floor",    # Random effects: 1 for intercept, floor for slope
                  data=radon)
res4 = sm4.fit()
res4.summary().tables[1]













  
    

      
      Coef.
      Std.Err.
      z
      P>|z|
      [0.025
      0.975]
    

  
  
    

      Intercept
      1.463
      0.054
      26.977
      0.000
      1.356
      1.569
    

    

      floor[T.ground]
      -0.681
      0.089
      -7.624
      0.000
      -0.856
      -0.506
    

    

      county Var
      0.122
      0.049
      
      
      
      
    

    

      county x floor[T.ground] Cov
      -0.040
      0.057
      
      
      
      
    

    

      floor[T.ground] Var
      0.118
      0.120
      
      
      
      
    

  











# slope estimate
res4.params["floor[T.ground]"]









-0.6810977572101952













# sigma-hat
np.sqrt(res4.scale)









0.7461559982563548













# standard deviation of the variability among county-specific Intercepts
county_var_int = res4.cov_re.loc["county", "county"]
np.sqrt(county_var_int)









0.3486722110725788













# standard deviation of the variability among county-specific slopes
county_var_slopes = res4.cov_re.loc["floor[T.ground]", "floor[T.ground]"]
np.sqrt(county_var_slopes)









0.343553974832034













# correlation between Intercept and slope group-level coefficients
county_floor_cov = res4.cov_re.loc["county", "floor[T.ground]"]
county_floor_cov / (np.sqrt(county_var_int)*np.sqrt(county_var_slopes))









-0.33723036077793395

















Discussion#




Alternative notations for hierarchical models#


    

  • IMPORT FROM Gelman & Hill Section 12.5 printout
    • 

  • watch the subscripts!
    • 







Computational challenges associated with hierarchical models#


    

  • centred vs. noncentred representations
    • 







Benefits of multilevel models#


    

  • TODO LIST
    • 

  • Better than repeated measures ANOVA because:
    

      

    • tells you the direction and magnitude of effect
      • 

    • can handle more multiple grouping scenarios (e.g. by-item, and by-student)
      • 

    • works for categorical predictors
      • 

    

    • 







Applications#


    

  • Need for hierarchical models often occurs in social sciences (better than ANOVA)
    • 

  • Hierarchical models are often used for Bayesian meta-analysis
    • 









Exercises#




Exercise: mod1u#


Same model as Example 3 but also include the predictor log_uranium.






import bambi as bmb

covariate_priors = {
    "floor": bmb.Prior("Normal", mu=0, sigma=10),
    "log_uranium": bmb.Prior("Normal", mu=0, sigma=10),
    "1|county": bmb.Prior("Normal", mu=0, sigma=bmb.Prior("Exponential", lam=1)),
    "sigma": bmb.Prior("Exponential", lam=1),
}

mod1u = bmb.Model(formula="log_radon ~ 1 + floor + (1|county) + log_uranium",
                  priors=covariate_priors,
                  data=radon)

mod1u









       Formula: log_radon ~ 1 + floor + (1|county) + log_uranium
        Family: gaussian
          Link: mu = identity
  Observations: 919
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 1.2246, sigma: 2.1322)
            floor ~ Normal(mu: 0.0, sigma: 10.0)
            log_uranium ~ Normal(mu: 0.0, sigma: 10.0)
        
        Group-level effects
            1|county ~ Normal(mu: 0.0, sigma: Exponential(lam: 1.0))
        
        Auxiliary parameters
            sigma ~ Exponential(lam: 1.0)













Exercise: pigs dataset#


https://bambinos.github.io/bambi/notebooks/multi-level_regression.html






import statsmodels.api as sm
dietox = sm.datasets.get_rdataset("dietox", "geepack").data
dietox













  
    

      
      Pig
      Evit
      Cu
      Litter
      Start
      Weight
      Feed
      Time
    

  
  
    

      0
      4601
      Evit000
      Cu000
      1
      26.5
      26.50000
      NaN
      1
    

    

      1
      4601
      Evit000
      Cu000
      1
      26.5
      27.59999
      5.200005
      2
    

    

      2
      4601
      Evit000
      Cu000
      1
      26.5
      36.50000
      17.600000
      3
    

    

      3
      4601
      Evit000
      Cu000
      1
      26.5
      40.29999
      28.500000
      4
    

    

      4
      4601
      Evit000
      Cu000
      1
      26.5
      49.09998
      45.200001
      5
    

    

      ...
      ...
      ...
      ...
      ...
      ...
      ...
      ...
      ...
    

    

      856
      8442
      Evit000
      Cu175
      24
      25.7
      73.19995
      83.800003
      8
    

    

      857
      8442
      Evit000
      Cu175
      24
      25.7
      81.69995
      99.800003
      9
    

    

      858
      8442
      Evit000
      Cu175
      24
      25.7
      90.29999
      115.200001
      10
    

    

      859
      8442
      Evit000
      Cu175
      24
      25.7
      96.00000
      133.200001
      11
    

    

      860
      8442
      Evit000
      Cu175
      24
      25.7
      103.50000
      151.400002
      12
    

  



861 rows × 8 columns










pigsmodel = bmb.Model("Weight ~ Time + (Time|Pig)", dietox)
pigsidata = pigsmodel.fit(random_seed=42)









Initializing NUTS using jitter+adapt_diag...





Multiprocess sampling (2 chains in 2 jobs)





NUTS: [sigma, Intercept, Time, 1|Pig_sigma, 1|Pig_offset, Time|Pig_sigma, Time|Pig_offset]







Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 9 seconds.





We recommend running at least 4 chains for robust computation of convergence diagnostics





The rhat statistic is larger than 1.01 for some parameters. This indicates problems during sampling. See https://arxiv.org/abs/1903.08008 for details













az.summary(pigsidata, var_names=["Intercept", "Time", "1|Pig_sigma", "Time|Pig_sigma", "sigma"])













  
    

      
      mean
      sd
      hdi_3%
      hdi_97%
      mcse_mean
      mcse_sd
      ess_bulk
      ess_tail
      r_hat
    

  
  
    

      Intercept
      15.762
      0.563
      14.735
      16.824
      0.027
      0.016
      444.0
      700.0
      1.00
    

    

      Time
      6.945
      0.079
      6.801
      7.096
      0.005
      0.003
      257.0
      456.0
      1.01
    

    

      1|Pig_sigma
      4.553
      0.447
      3.754
      5.404
      0.020
      0.012
      507.0
      900.0
      1.00
    

    

      Time|Pig_sigma
      0.662
      0.062
      0.550
      0.777
      0.003
      0.001
      478.0
      796.0
      1.00
    

    

      sigma
      2.458
      0.064
      2.332
      2.571
      0.001
      0.002
      1926.0
      1213.0
      1.00
    

  











Exercise: educational data#


cf. https://mc-stan.org/users/documentation/case-studies/tutorial_rstanarm.html


1.1 Data example
We will be analyzing the Gcsemv dataset (Rasbash et al. 2000) from the mlmRev package in R.
The data include the General Certificate of Secondary Education (GCSE) exam scores of 1,905 students from 73 schools in England on a science subject. The Gcsemv dataset consists of the following 5 variables:


    

  • school: school identifier
    • 

  • student: student identifier
    • 

  • gender: gender of a student (M: Male, F: Female)
    • 

  • written: total score on written paper
    • 

  • course: total score on coursework paper
    • 







# import pyreadr
# path = "/Users/ivan/Desktop/stats stuff from desktop/Current Bayesian/Hierarchical models/mlmRev"
# Gcsemv_r = pyreadr.read_r(path + '/data/Gcsemv.rda')
# Gcsemv_r["Gcsemv"].dropna().to_csv("datasets/exercises/gcsemv.csv", index=False)

gcsemv = pd.read_csv("datasets/exercises/gcsemv.csv")
gcsemv.head()













  
    

      
      school
      student
      gender
      written
      course
    

  
  
    

      0
      20920
      27
      F
      39.0
      76.8
    

    

      1
      20920
      31
      F
      36.0
      87.9
    

    

      2
      20920
      42
      M
      16.0
      44.4
    

    

      3
      20920
      101
      F
      49.0
      89.8
    

    

      4
      20920
      113
      M
      25.0
      17.5
    

  











import bambi as bmb
m1 = bmb.Model(formula="course ~ 1 + (1 | school)", data=gcsemv)
m1









       Formula: course ~ 1 + (1 | school)
        Family: gaussian
          Link: mu = identity
  Observations: 1523
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 73.3814, sigma: 41.0781)
        
        Group-level effects
            1|school ~ Normal(mu: 0.0, sigma: HalfNormal(sigma: 41.0781))
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 16.4312)













idata_m1 = m1.fit(random_seed=42)









Initializing NUTS using jitter+adapt_diag...





Multiprocess sampling (2 chains in 2 jobs)





NUTS: [sigma, Intercept, 1|school_sigma, 1|school_offset]







Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 3 seconds.





We recommend running at least 4 chains for robust computation of convergence diagnostics













az.summary(idata_m1)













  
    

      
      mean
      sd
      hdi_3%
      hdi_97%
      mcse_mean
      mcse_sd
      ess_bulk
      ess_tail
      r_hat
    

  
  
    

      sigma
      13.981
      0.255
      13.528
      14.453
      0.004
      0.006
      3605.0
      1232.0
      1.0
    

    

      Intercept
      73.725
      1.141
      71.659
      75.971
      0.051
      0.026
      495.0
      839.0
      1.0
    

    

      1|school_sigma
      8.873
      0.941
      7.225
      10.726
      0.044
      0.023
      476.0
      773.0
      1.0
    

    

      1|school[20920]
      -6.838
      5.149
      -17.271
      2.250
      0.108
      0.125
      2280.0
      1411.0
      1.0
    

    

      1|school[22520]
      -15.535
      2.161
      -19.292
      -11.257
      0.063
      0.042
      1200.0
      1495.0
      1.0
    

    

      ...
      ...
      ...
      ...
      ...
      ...
      ...
      ...
      ...
      ...
    

    

      1|school[76531]
      -11.327
      5.122
      -21.116
      -2.152
      0.100
      0.119
      2638.0
      1524.0
      1.0
    

    

      1|school[76631]
      2.238
      2.772
      -3.204
      7.222
      0.069
      0.064
      1607.0
      1113.0
      1.0
    

    

      1|school[77207]
      -3.114
      3.302
      -9.791
      2.608
      0.070
      0.075
      2207.0
      1471.0
      1.0
    

    

      1|school[84707]
      4.075
      7.575
      -8.578
      19.934
      0.146
      0.181
      2711.0
      1299.0
      1.0
    

    

      1|school[84772]
      8.655
      3.769
      1.508
      15.533
      0.076
      0.095
      2476.0
      1198.0
      1.0
    

  



76 rows × 9 columns










m3 = bmb.Model(formula="course ~ gender + (1 + gender|school)", data=gcsemv)
m3









       Formula: course ~ gender + (1 + gender|school)
        Family: gaussian
          Link: mu = identity
  Observations: 1523
        Priors: 
    target = mu
        Common-level effects
            Intercept ~ Normal(mu: 73.3814, sigma: 53.4663)
            gender ~ Normal(mu: 0.0, sigma: 83.5292)
        
        Group-level effects
            1|school ~ Normal(mu: 0.0, sigma: HalfNormal(sigma: 53.4663))
            gender|school ~ Normal(mu: 0.0, sigma: HalfNormal(sigma: 83.5292))
        
        Auxiliary parameters
            sigma ~ HalfStudentT(nu: 4.0, sigma: 16.4312)













idata_m3 = m3.fit(random_seed=42)









Initializing NUTS using jitter+adapt_diag...





Multiprocess sampling (2 chains in 2 jobs)





NUTS: [sigma, Intercept, gender, 1|school_sigma, 1|school_offset, gender|school_sigma, gender|school_offset]







Sampling 2 chains for 1_000 tune and 1_000 draw iterations (2_000 + 2_000 draws total) took 6 seconds.





We recommend running at least 4 chains for robust computation of convergence diagnostics













Exercise: sleepstudy dataset#


    

  • Description: Contains reaction times of subjects under sleep deprivation conditions.
    • 

  • Source: Featured in the R package lme4.
    • 

  • Application: Demonstrates linear mixed-effects modeling with random slopes and intercepts.
    • 



Links:







sleepstudy = bmb.load_data("sleepstudy")
sleepstudy









---------------------------------------------------------------------------
OSError                                   Traceback (most recent call last)
Cell In[74], line 1
----> 1 sleepstudy = bmb.load_data("sleepstudy")
      2 sleepstudy

File /opt/hostedtoolcache/Python/3.10.19/x64/lib/python3.10/site-packages/bambi/data/datasets.py:272, in load_data(dataset, data_home)
    270         checksum = _sha256(file_path)
    271         if datafile.checksum != checksum:
--> 272             raise IOError(
    273                 f"{file_path} has an SHA256 checksum ({checksum}) differing from expected "
    274                 f"({datafile.checksum}), file may be corrupted. Run `bambi.clear_data_home()` "
    275                 "and try again, or please open an issue."
    276             )
    277     return pd.read_csv(file_path)
    278 else:

OSError: /home/runner/bambi_data/sleepstudy.csv has an SHA256 checksum (e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855) differing from expected (0a002bec8be2fa9d40dbbf3d5038e614d113a4fd5bf8813f6f4271c3d6294675), file may be corrupted. Run `bambi.clear_data_home()` and try again, or please open an issue.













Exercise: tadpoles (BONUS)#


https://www.youtube.com/watch?v=iwVqiiXYeC4


logistic regression model









EXTRA MATERIAL#






    
    

                

              

              
              
              
              
                
              
            

            
            
              
                



  

  

     Contents