Section 2.3 — Inventory of discrete distributions

This notebook contains all the code examples from Section 2.3 Inventory of discrete distributions of the No Bullshit Guide to Statistics.

Notebook setup

# load Python modules
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Figures setup
sns.set_theme(
    context="paper",
    style="whitegrid",
    palette="colorblind",
    rc={'figure.figsize': (6,2)},
)

%config InlineBackend.figure_format = 'retina'

# simple float __repr__
np.set_printoptions(legacy='1.25')

# set random seed for repeatability
np.random.seed(42)

%pip install -q ministats

Note: you may need to restart the kernel to use updated packages.

from ministats import plot_pmf

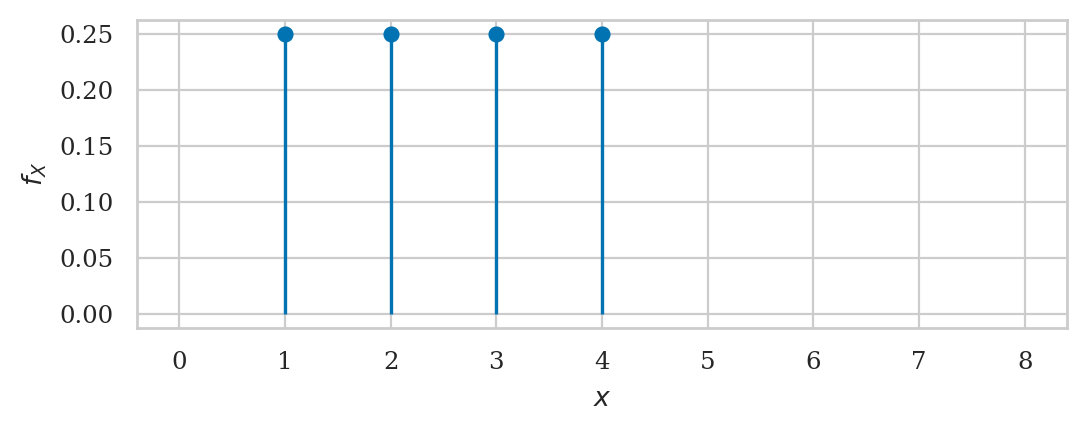
Discrete uniform distribution

from scipy.stats import randint

alpha = 1
beta = 4
rvR = randint(alpha, beta+1)

Note the +1 we added to the second argument.

rvR.mean()

2.5

rvR.var()

1.25

The limits of the sample space of the random variable rvR can be obtained by calling its .support() method.

Probability mass function

plot_pmf(rvR, xlims=[0,8+1]);

rvR.support()

(1, 4)

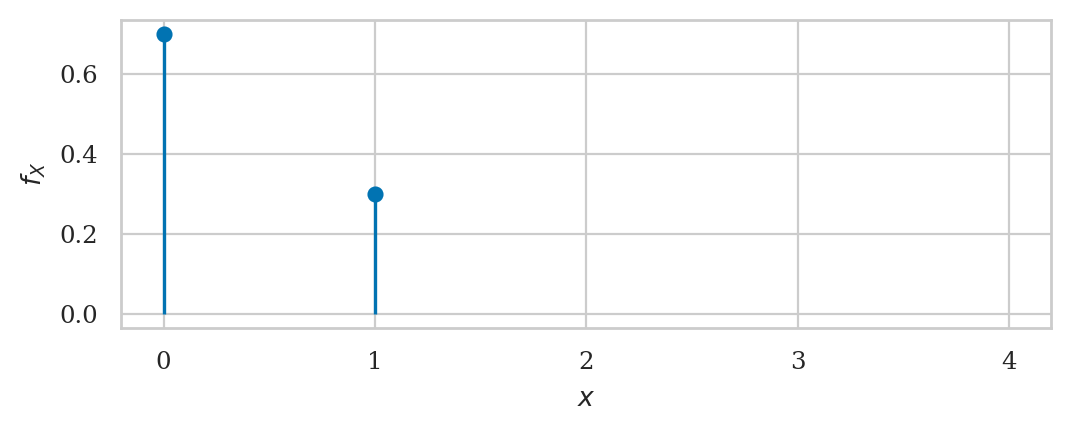
Bernoulli distribution

from scipy.stats import bernoulli

rvB = bernoulli(p=0.3)

rvB.support()

(0, 1)

rvB.mean(), rvB.var()

(0.3, 0.21)

rvB.rvs(10)

array([0, 1, 1, 0, 0, 0, 0, 1, 0, 1])

plot_pmf(rvB, xlims=[0,5]);

Mathematical interlude: counting combinations

Factorials

TODO explain + math formula

from scipy.special import factorial

factorial(4)

24.0

# # ALT.
# from math import factorial
# factorial(4)

The factorial of \(0\) is defined as 1: \(0!=1\).

factorial(0)

1.0

The factorial function grows grows very quickly:

[factorial(n) for n in [5, 6, 7, 8, 9, 10, 11, 12, 13]]

[120.0,
 720.0,
 5040.0,
 40320.0,
 362880.0,
 3628800.0,
 39916800.0,
 479001600.0,
 6227020800.0]

Combinations

TODO explain + math formula

from scipy.special import comb

comb(5, 2)

10.0

from itertools import combinations

list(combinations({1,2,3,4,5}, 2))

[(1, 2),
 (1, 3),
 (1, 4),
 (1, 5),
 (2, 3),
 (2, 4),
 (2, 5),
 (3, 4),
 (3, 5),
 (4, 5)]

Exercises

from scipy.special import comb

comb(12,6)

924.0

from scipy.special import comb

comb(52,5)

2598960.0

Links

• https://en.wikipedia.org/wiki/Factorials

• https://en.wikipedia.org/wiki/Combinations

• https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.factorial.html

• https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.comb.html

• https://docs.python.org/3/library/itertools.html#itertools.combinations

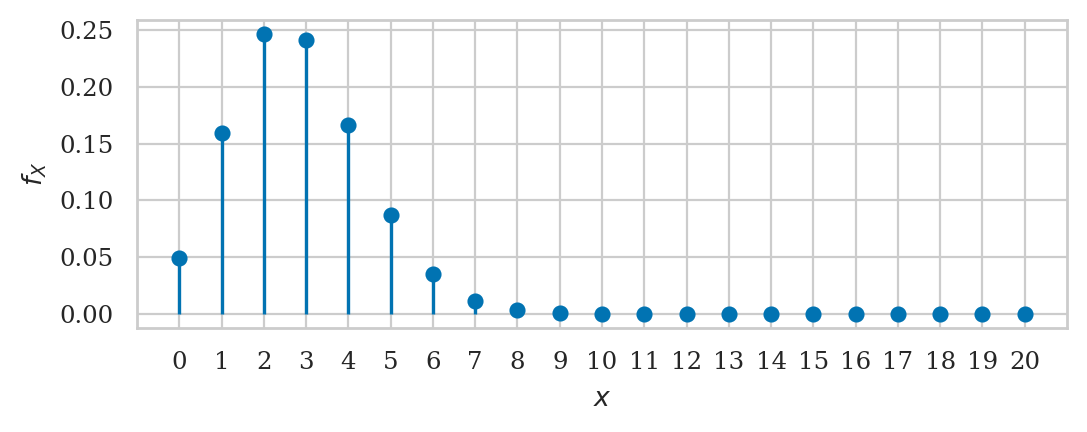
Binomial distribution

We’ll use the name rvX because rvB was already used for the Bernoulli random variable above.

from scipy.stats import binom

n = 20
p = 0.14
rvX = binom(n,p)

rvX.support()

(0, 20)

rvX.mean(), rvX.var()

(2.8000000000000003, 2.4080000000000004)

plot_pmf(rvX, xlims=[0,21]);

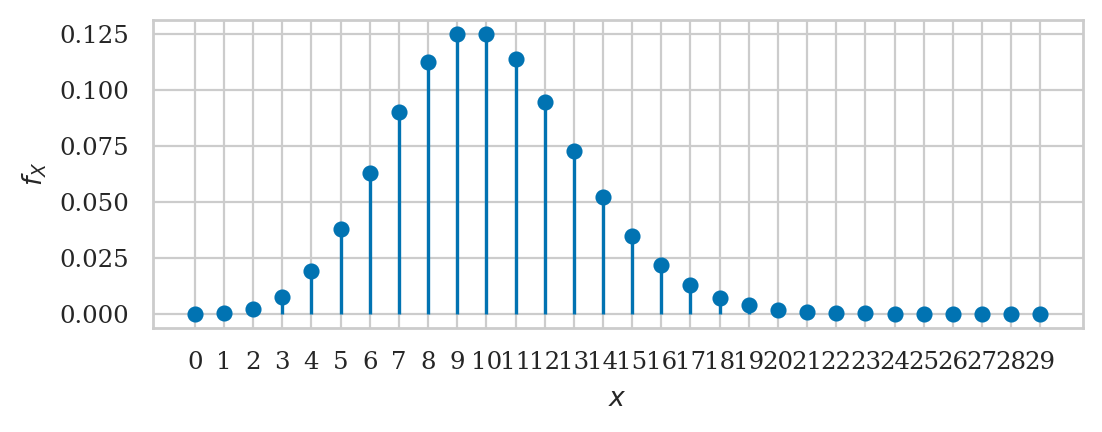
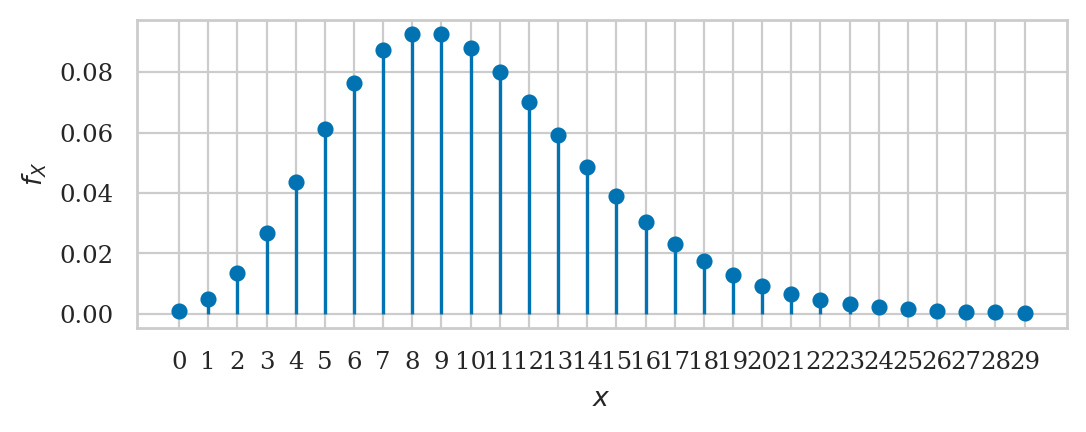
Poisson distribution

from scipy.stats import poisson
lam = 10
rvP = poisson(lam)

rvP.pmf(8)

0.11259903214902009

rvP.cdf(8)

0.3328196787507191

## ALT. way to compute the value F_P(8) =
# sum([rvP.pmf(x) for x in range(0,8+1)])

plot_pmf(rvP, xlims=[0,30]);

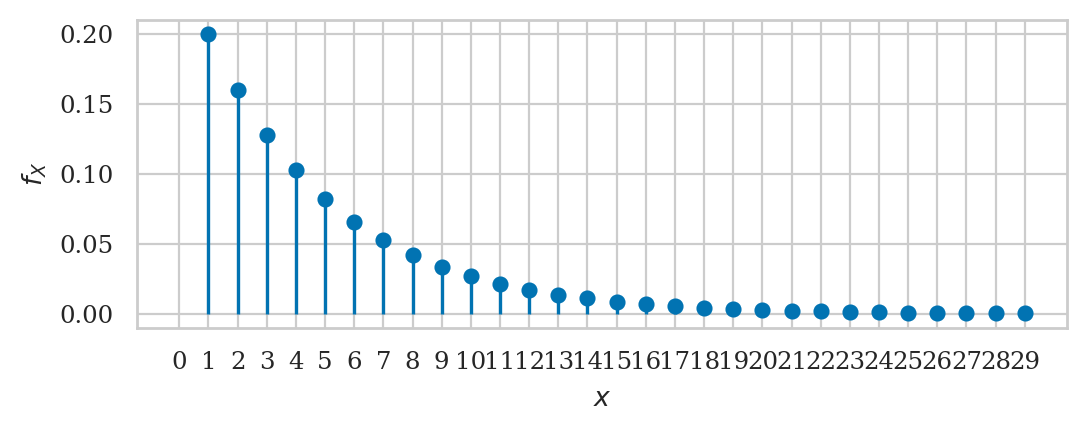
Geometric distribution

from scipy.stats import geom

rvG = geom(p = 0.2)

rvG.support()

(1, inf)

rvG.mean(), rvG.var()

(5.0, 20.0)

plot_pmf(rvG, xlims=[0,30]);

Negative binomial distribution

from scipy.stats import nbinom

r = 10
p = 0.5
rvN = nbinom(r,p)

rvN.support()

(0, inf)

rvN.mean(), rvN.var()

(10.0, 20.0)

plot_pmf(rvN, xlims=[0,30]);

Computer models for discrete distributions

TODO table models

TODO table methods

Building computer models for random variables

# import the model family
from scipy.stats import randint

# choose parameters
alpha = 1  # start at 1
beta = 4   # stop at 4

# create the rv object
rvR = randint(alpha, beta+1)

Note the +1 we added to the second argument.

rvR.mean()

2.5

# verify using formula
(alpha + beta) / 2

2.5

rvR.var()

1.25

# verify using formula
((beta + 1 - alpha)**2 - 1) / 12

1.25

rvR.std()

1.118033988749895

The limits of the sample space of the random variable rvR can be obtained by calling its .support() method.

rvR.support()

(1, 4)

Probability calculations

rvR.pmf(1) + rvR.pmf(2) + rvR.pmf(3)

0.75

[rvR.pmf(r) for r in range(1,3+1)]

[0.25, 0.25, 0.25]

sum([rvR.pmf(r) for r in range(1,3+1)])

0.75

rvR.cdf(3)

0.75

Plotting distributions

Probability mass function

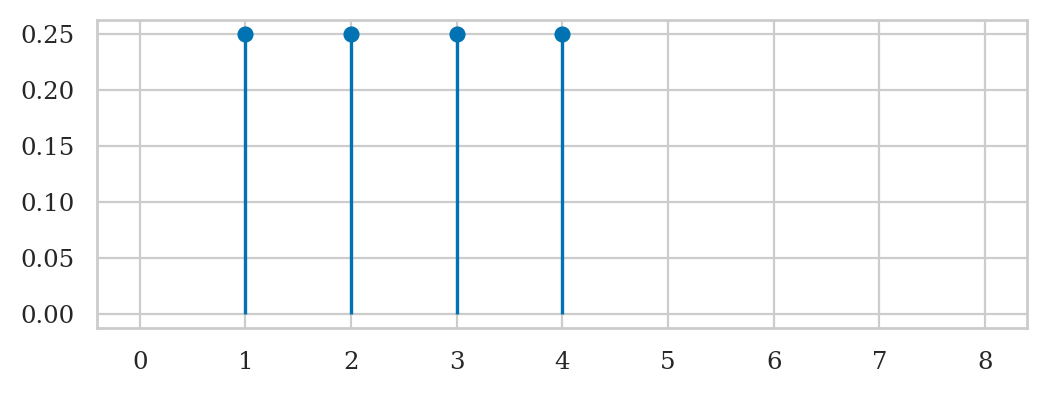
To create a stem-plot of the probability mass function \(f_R\), we can use the following three-step procedure:

1. Create a range of inputs rs for the plot.

2. Compute the value of \(f_R =\) rvR for each of the inputs and store the results as list of values fRs.

3. Plot the values fRs by calling the function plt.stem(rs, fRs).

import matplotlib.pyplot as plt

rs = range(0, 8+1)
fRs = rvR.pmf(rs)
fRs = np.where(fRs == 0, np.nan, fRs)  # set zero fRs to np.nan
plt.stem(rs, fRs, basefmt=" ");

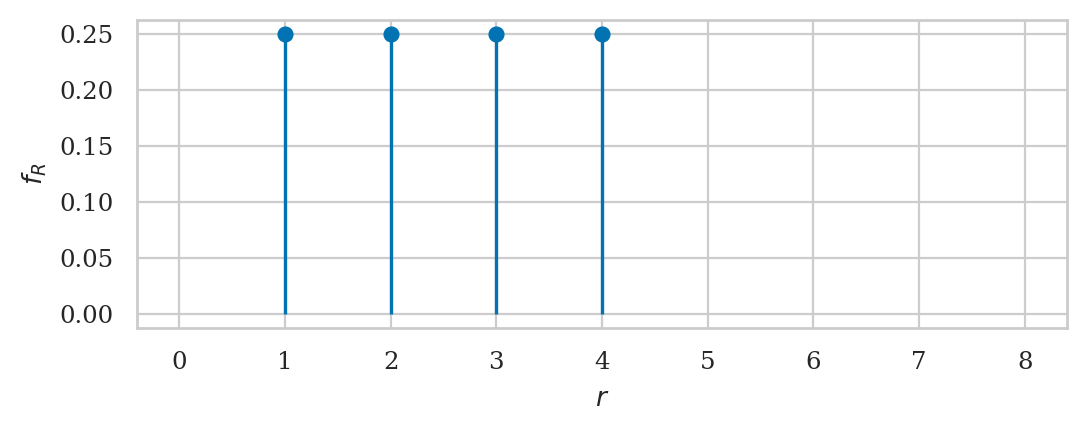
Note, we used the np.where statement to replace zero entries in the list fRs to the special Not a Number (np.nan) values, which excludes them from the plot. This is arguably a cleaner representation of the PMF plot: the function is only defined for the sample space \(\mathcal{R} = \{1,2,3,4\}\).

An alternative ,,,

# ALT. using helper function
from ministats import plot_pmf

plot_pmf(rvR, xlims=[0,8+1], rv_name="R");

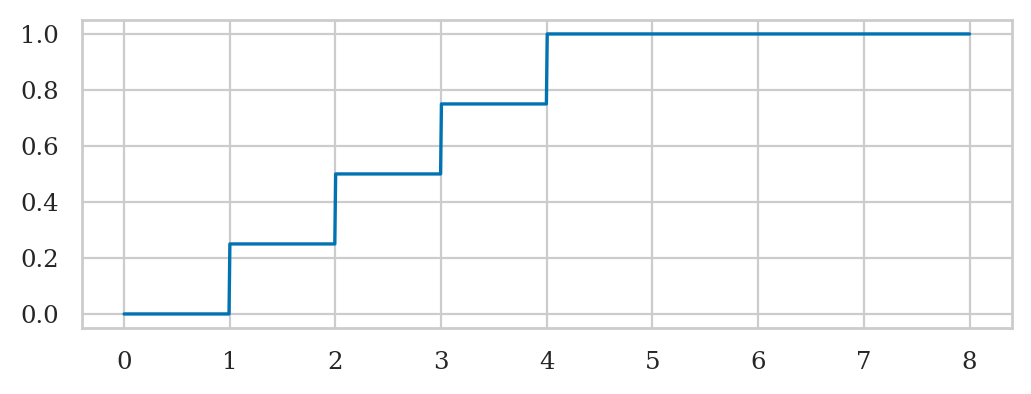
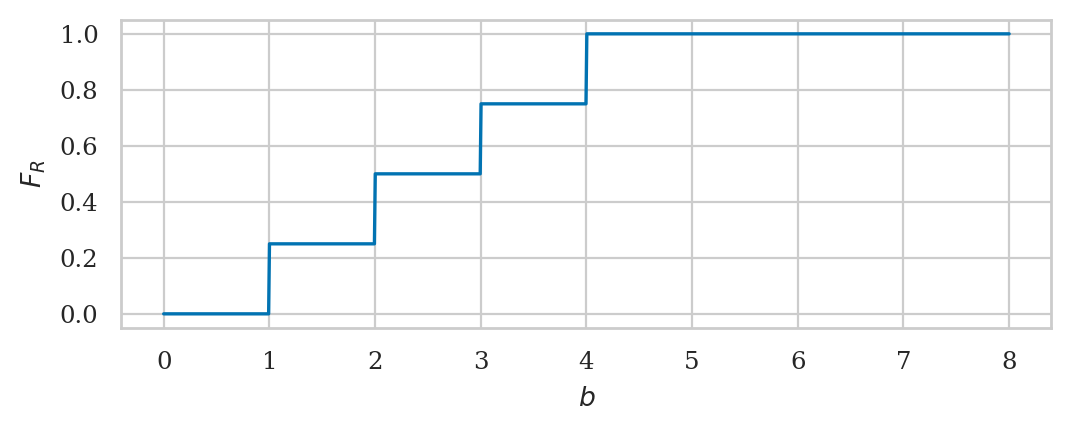
Cumulative distribution function

import numpy as np
import seaborn as sns

bs = np.linspace(0, 8, 1000)
FRs = rvR.cdf(bs)
sns.lineplot(x=bs, y=FRs);

# ALT. using helper function
from ministats import plot_cdf

plot_cdf(rvR, xlims=[0,8], rv_name="R");

Generating random observations

Let’s generate 10 random observations from random variable rvR:

np.random.seed(43)

rvR.rvs(10)

array([1, 1, 4, 2, 2, 3, 1, 4, 2, 4])

Explanations

Binomial coefficient formula explained

n = 6

[int(comb(n,k)) for k in range(0,n+1)]

[1, 6, 15, 20, 15, 6, 1]

We can draw Pascal’s triangle by by repeating the above calculation for several values of n.

for n in range(0,10):
    row_ints = [int(comb(n,k)) for k in range(0,n+1)]
    row_str = str(row_ints)
    row_str = row_str.replace("[","").replace("]","").replace(",", "  ")
    row_str = row_str.center(60)
    print(row_str)

                             1                              
                           1   1                            
                         1   2   1                          
                       1   3   3   1                        
                     1   4   6   4   1                      
                  1   5   10   10   5   1                   
                1   6   15   20   15   6   1                
             1   7   21   35   35   21   7   1              
           1   8   28   56   70   56   28   8   1           
       1   9   36   84   126   126   84   36   9   1        

Geometric sums

r = 0.3

sum([r**n for n in range(0,100)])

1.4285714285714288

1 / (1 - r)

1.4285714285714286

Discussion

Relations between distributions

Exercises

Exercise XX

from scipy.stats import poisson
lam = 20
rvH = poisson(lam)

# a) Pr(H in {20,21,22}) 
rvH.pmf(20) + rvH.pmf(21) + rvH.pmf(22)

0.2503540762867847

# b) Pr({16≤H≤24})
rvH.cdf(24) - rvH.cdf(16-1)

0.6867142435340193

# c) F_H^{-1}(0.95)
rvH.ppf(0.95)

28.0

Links