Section 4.2 — Multiple linear regression

Section 4.2 — Multiple linear regression#

This notebook contains the code examples from Section 4.2 Multiple linear regression from the No Bullshit Guide to Statistics.

Notebook setup#

# load Python modules
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Figures setup
plt.clf()  # needed otherwise `sns.set_theme` doesn't work
from plot_helpers import RCPARAMS
# RCPARAMS.update({"figure.figsize": (10, 4)})   # good for screen
RCPARAMS.update({"figure.figsize": (5, 2.3)})  # good for print
sns.set_theme(
    context="paper",
    style="whitegrid",
    palette="colorblind",
    rc=RCPARAMS,
)

# High-resolution please
%config InlineBackend.figure_format = "retina"

# Where to store figures
DESTDIR = "figures/lm/multiple"

<Figure size 640x480 with 0 Axes>

# set random seed for repeatability
np.random.seed(42)

Definitions#

Doctors dataset#

doctors = pd.read_csv("../datasets/doctors.csv")
doctors.shape

(156, 9)

doctors.head()
permit loc work hours caf alc weed exrc score
0 93273 rur hos 21 2 0 5.0 0.0 63
1 90852 urb cli 74 26 20 0.0 4.5 16
2 92744 urb hos 63 25 1 0.0 7.0 58
3 73553 urb eld 77 36 4 0.0 2.0 55
4 82441 rur cli 36 22 9 0.0 7.5 47

Multiple linear regression model#

\(\newcommand{\Err}{ {\Large \varepsilon}}\)

\[ Y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p + \Err, \]

where \(p\) is the number of predictors and \(\Err\) represents Gaussian noise \(\Err \sim \mathcal{N}(0,\sigma)\).

Model assumptions#

  • (LIN)

  • (INDEPɛ)

  • (NORMɛ)

  • (EQVARɛ)

  • (NOCOL)

Example: linear model for doctors’ sleep scores#

We want to know the influence of drinking alcohol, smoking weed, and exercise on sleep score?

import statsmodels.formula.api as smf

formula = "score ~ 1 + alc + weed + exrc"
lm2 = smf.ols(formula, data=doctors).fit()
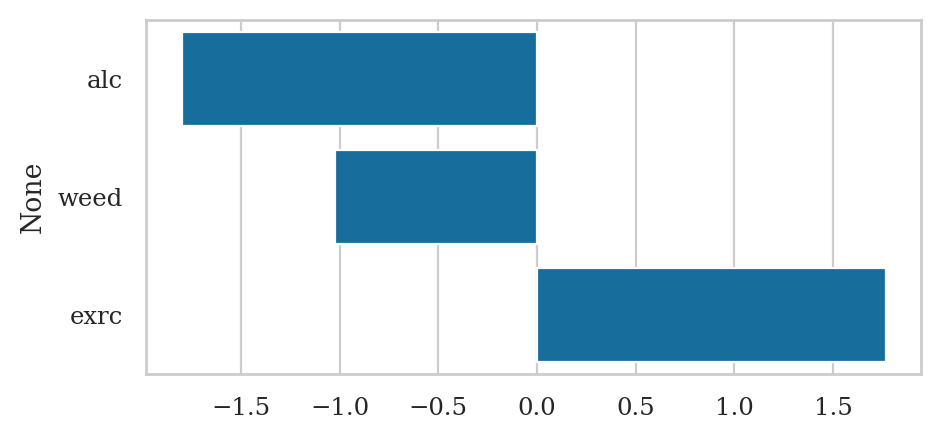
lm2.params

Intercept    60.452901
alc          -1.800101
weed         -1.021552
exrc          1.768289
dtype: float64

sns.barplot(x=lm2.params.values[1:],
            y=lm2.params.index[1:]);
../_images/c2901827573e4cd9e622dd9fdb10312e7f0e157508dfebe792139c4056cfc3c5.png

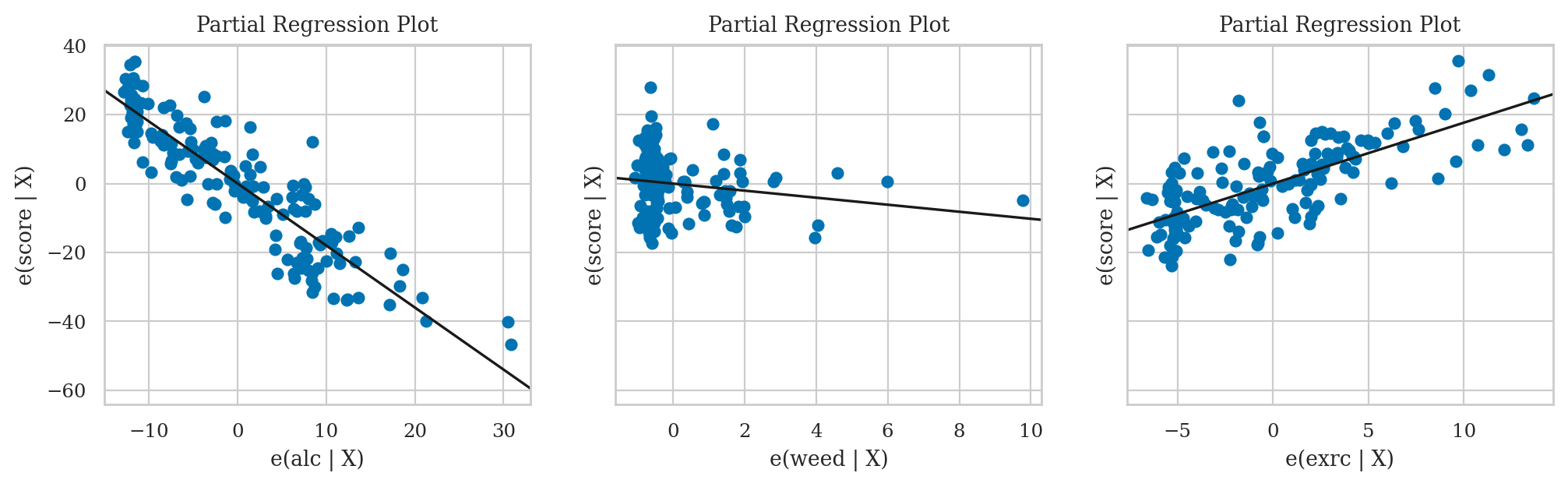
Partial regression plots#

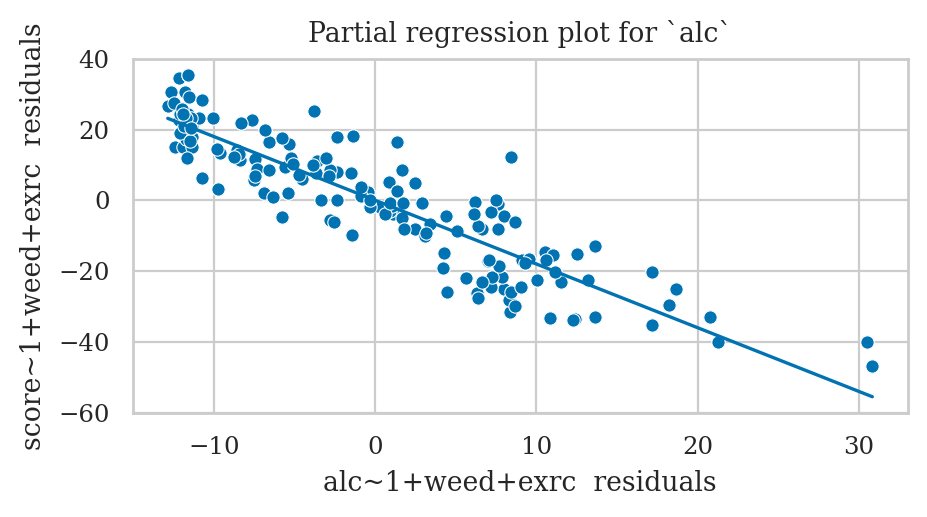
Partial regression plot for the predictor alc#

Step 1: Obtain the data for the x-axis, residuals of the model alc ~ 1 + others

#######################################################
lm_alc = smf.ols("alc~1+weed+exrc", data=doctors).fit()
xrs = lm_alc.resid

Step 2: Obtain the data for the y-axis, residuals of the model score ~ 1 + others

#######################################################
lm_score=smf.ols("score~1+weed+exrc",data=doctors).fit()
yrs = lm_score.resid

Step 3: Fit a linear model for the y-residuals versus the x-residuals.

dfrs = pd.DataFrame({"xrs": xrs, "yrs": yrs})
lm_resids = smf.ols("yrs ~ 1 + xrs", data=dfrs).fit()

Step 4: Draw a scatter plot of the residuals and the best-fitting linear model to the residuals.

from ministats import plot_reg

ax = sns.scatterplot(x=xrs, y=yrs, color="C0")
plot_reg(lm_resids, ax=ax);
ax.set_xlabel("alc~1+weed+exrc  residuals")
ax.set_ylabel("score~1+weed+exrc  residuals")
ax.set_title("Partial regression plot for `alc`");
../_images/dc868736548825a261412e882c38951c8584b9afd1d03aacc99560a1cafbe7ae.png

The slope parameter for the residuals model is the same as the slope parameter of the alc predictor in the original model lm2.

lm_resids.params["xrs"], lm2.params["alc"]

(-1.8001013152459409, -1.8001013152459384)

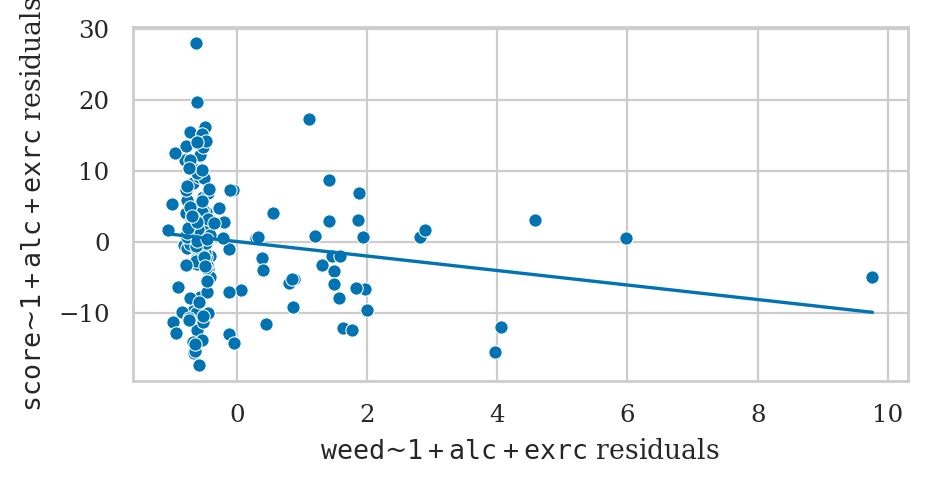
Partial regression plot for the predictor weed#

from ministats import plot_partreg
plot_partreg(lm2, pred="weed");
../_images/91a31a1d167aa65bc9aefc5065ae08f623b8d2af3d32a40677fb5fda05f83752.png

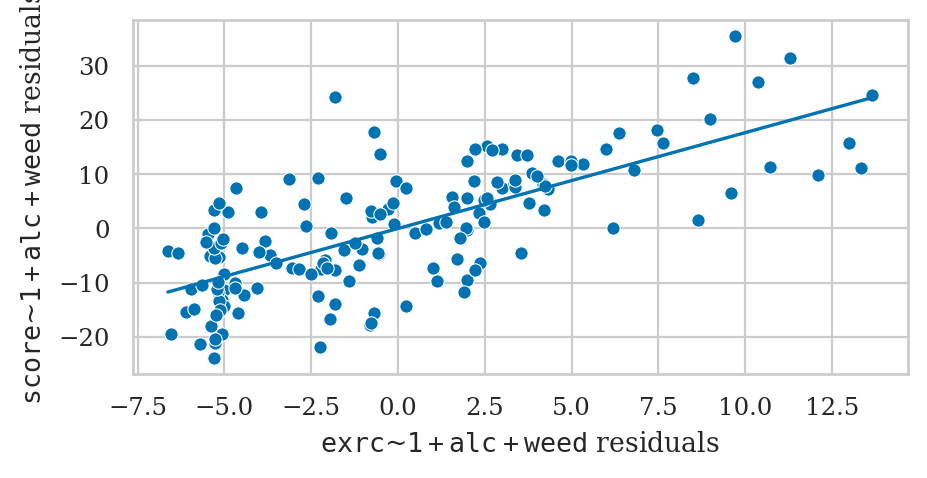
Partial regression plot for the predictor exrc#

plot_partreg(lm2, pred="exrc");
../_images/e7aa1a3a076c96248b15c885e3219b2ade19fc3a14926b810accb33e00bc755d.png

(BONUS TOPIC) Partial regression plots using statsmodels#

The function plot_partregress defined in statsmodels.graphics.api performs the same steps as the function plot_partreg we used above. but is a little more awkward to use.

When calling the function plot_partregress, you must provide the following arguments:

  • the outcome variable (endog)

  • the predictor you’re interested in (exog_i)

  • the predictors you want to regress out (exog_others)

  • the data frame that contains all these variable (data)

from statsmodels.graphics.api import plot_partregress

with plt.rc_context({"figure.figsize":(12,3)}):
    fig, (ax1, ax2, ax3) = plt.subplots(1,3, sharey=True)
    plot_partregress("score", "alc",  exog_others=["weed", "exrc"], data=doctors, obs_labels=False, ax=ax1)
    plot_partregress("score", "weed", exog_others=["alc",  "exrc"], data=doctors, obs_labels=False, ax=ax2)
    plot_partregress("score", "exrc", exog_others=["alc",  "weed"], data=doctors, obs_labels=False, ax=ax3)
../_images/0614de6d56ff3811cfb7b9c0da0cf5bd2eec0e3e98c8fbb49309e6f7e0ec6b7c.png

The notation \(|\textrm{X}\) you see in the axis labels stands for “given all other predictors,” and is different for each subplot. For example, in the leftmost partial regression plot, the predictor we are focussing on is alc, so the other variables (\(|\textrm{X}\)) are weed and exrc.

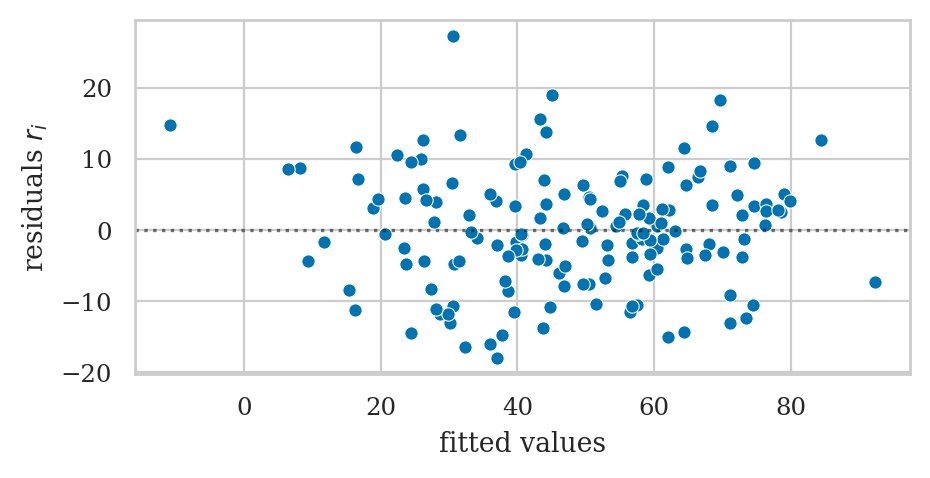
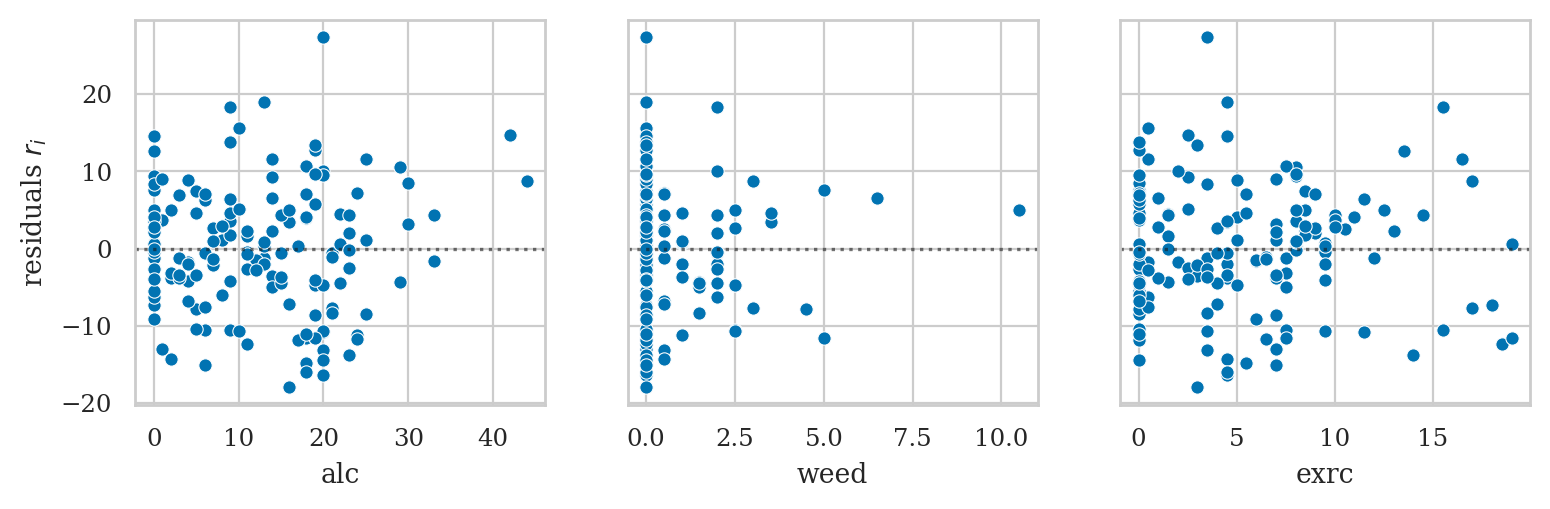
Plot residuals#

from ministats import plot_resid
plot_resid(lm2);
../_images/3d821f5eafb77ca820223a292a6bf9332ebde30989956897d22f4b9d3a4de039.png 
fig, (ax1,ax2,ax3) = plt.subplots(1, 3, sharey=True, figsize=(9,2.5))
plot_resid(lm2, pred="alc",  ax=ax1)
plot_resid(lm2, pred="weed", ax=ax2)
plot_resid(lm2, pred="exrc", ax=ax3);
../_images/aa2429eb57e031a0ff18dcf4028aa4f35e7bf1d1e8bc07f3c629db5b934ce027.png

Model summary table#

lm2.summary()
OLS Regression Results
Dep. Variable: score R-squared: 0.842
Model: OLS Adj. R-squared: 0.839
Method: Least Squares F-statistic: 270.3
Date: Fri, 15 Nov 2024 Prob (F-statistic): 1.05e-60
Time: 04:23:52 Log-Likelihood: -547.63
No. Observations: 156 AIC: 1103.
Df Residuals: 152 BIC: 1115.
Df Model: 3
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 60.4529 1.289 46.885 0.000 57.905 63.000
alc -1.8001 0.070 -25.726 0.000 -1.938 -1.662
weed -1.0216 0.476 -2.145 0.034 -1.962 -0.081
exrc 1.7683 0.138 12.809 0.000 1.496 2.041
Omnibus: 1.140 Durbin-Watson: 1.828
Prob(Omnibus): 0.565 Jarque-Bera (JB): 0.900
Skew: 0.182 Prob(JB): 0.638
Kurtosis: 3.075 Cond. No. 31.2


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Explanations#

Nonlinear terms in linear regression#

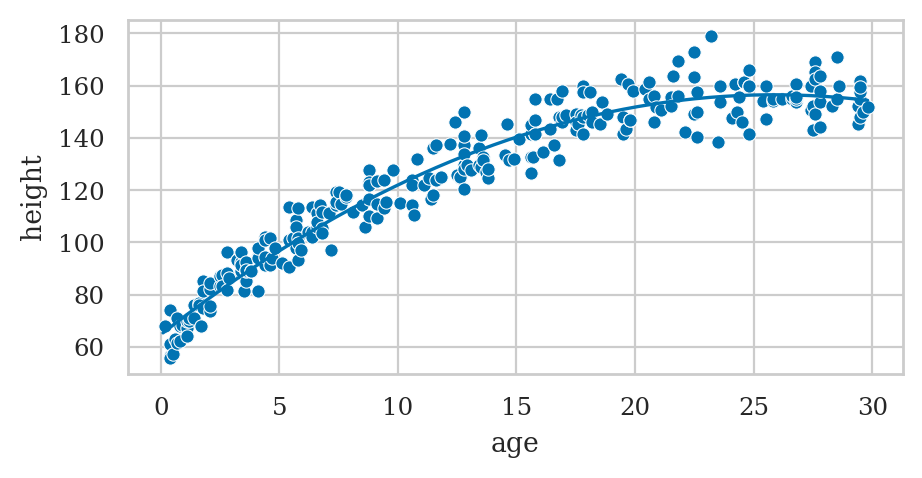
Example: polynomial regression#

howell30 = pd.read_csv("../datasets/howell30.csv")
len(howell30)

270

# Fit quadratic model
formula2 = "height ~ 1 + age + np.square(age)"
lmq = smf.ols(formula2, data=howell30).fit()
lmq.params

Intercept         64.708568
age                7.100854
np.square(age)    -0.137302
dtype: float64

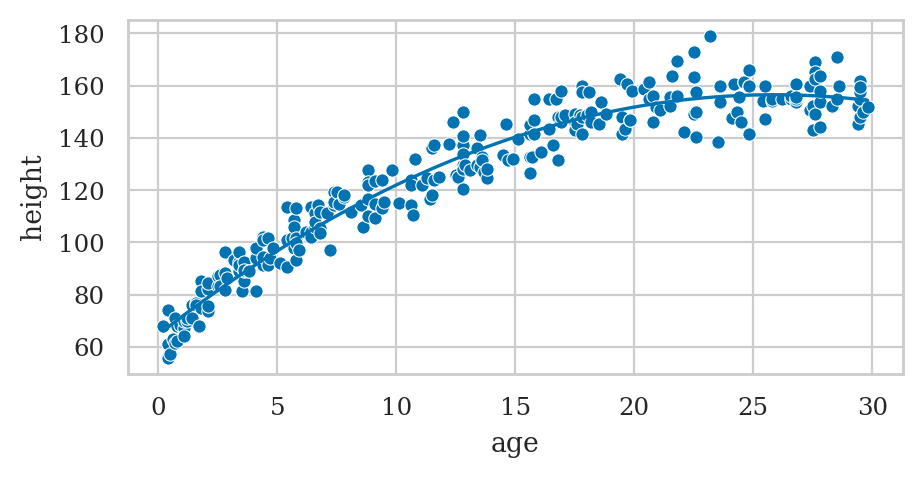
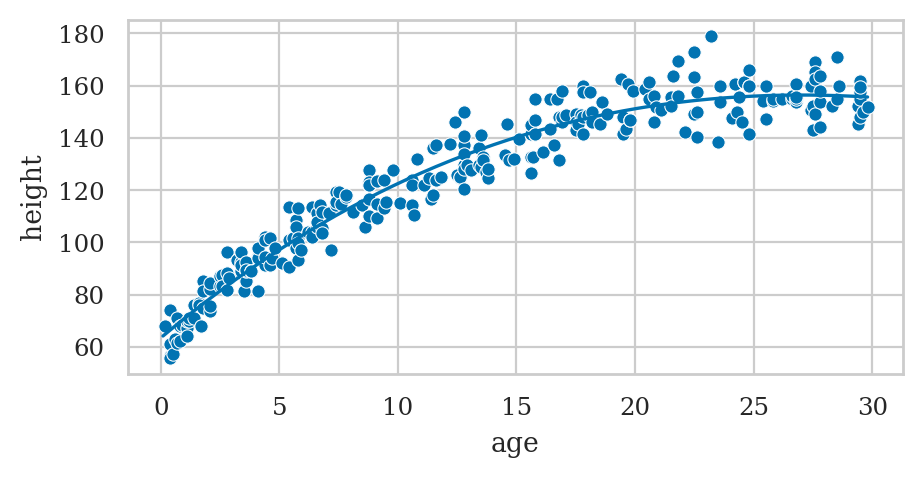
# Plot the data
sns.scatterplot(data=howell30, x="age", y="height");

# Plot the best-fit quadratic model
intercept, b_lin, b_quad = lmq.params
ages = np.linspace(0.1, howell30["age"].max())
heighthats = intercept + b_lin*ages + b_quad*ages**2
sns.lineplot(x=ages, y=heighthats, color="b");
../_images/19933bc6382731cfc6bf163482caf8fddfd2d85289620d52a1f3410b382464a6.png 
# ALT. using `plot_reg` function
from ministats import plot_reg
plot_reg(lmq);
../_images/dc5d1a54a94cc2abd22d068108ccbdac1b70ebcc79cf96a51496c938cc992548.png

Feature engineering and transformed variables#

Bonus example: polynomial regression up to degree 3#

formula3 = "height ~ 1 + age + np.power(age,2) + np.power(age,3)"
exlm3 = smf.ols(formula3, data=howell30).fit()
exlm3.params

Intercept           63.461484
age                  7.636139
np.power(age, 2)    -0.183218
np.power(age, 3)     0.001033
dtype: float64

sns.scatterplot(data=howell30, x="age", y="height")
sns.lineplot(x=ages, y=exlm3.predict({"age":ages}));
../_images/6571e8ca4950c295800978b55cfff676ba0c12b2ad949a11d43faa79c231c820.png

Discussion#

Exercises#

Exercise E??: marketing dataset#

marketing = pd.read_csv("../datasets/exercises/marketing.csv")
formula_mkt = "sales ~ 1 + youtube + facebook + newspaper"
lm_mkt2 = smf.ols(formula_mkt, data=marketing).fit()
lm_mkt2.params

Intercept    3.526667
youtube      0.045765
facebook     0.188530
newspaper   -0.001037
dtype: float64