Section 5.4 — Bayesian linear models

Section 5.4 — Bayesian linear models#

This notebook contains the code examples from Section 5.4 Bayesian linear models from the No Bullshit Guide to Statistics.

See also examples in:

Notebook setup#

# load Python modules
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# Figures setup
plt.clf()  # needed otherwise `sns.set_theme` doesn"t work
from plot_helpers import RCPARAMS
RCPARAMS.update({"figure.figsize": (5, 3)})   # good for screen
# RCPARAMS.update({"figure.figsize": (5, 1.6)})  # good for print
sns.set_theme(
    context="paper",
    style="whitegrid",
    palette="colorblind",
    rc=RCPARAMS,
)

# High-resolution please
%config InlineBackend.figure_format = "retina"

# Where to store figures
DESTDIR = "figures/bayesian/lms"

<Figure size 640x480 with 0 Axes>

# set random seed for repeatability
np.random.seed(42)

Simple linear regression using PyMC#

import pymc as pm
import numpy as np
import arviz as az

# Simulated data
np.random.seed(42)
x = np.random.normal(0, 1, 100)
y = 3 + 2 * x + np.random.normal(0, 1, 100)

# Bayesian Linear Regression Model
with pm.Model() as model:
    # Priors
    beta0 = pm.Normal("beta0", mu=0, sigma=10)
    beta1 = pm.Normal("beta1", mu=0, sigma=10)
    sigma = pm.HalfNormal("sigma", sigma=1)
    
    # Likelihood
    mu = beta0 + beta1 * x
    y_obs = pm.Normal("y_obs", mu=mu, sigma=sigma, observed=y)
    
    # Sampling
    trace = pm.sample(2000, return_inferencedata=True)

WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.

---------------------------------------------------------------------------
ImportError                               Traceback (most recent call last)
Cell In[4], line 1
----> 1 import pymc as pm
      2 import numpy as np
      3 import arviz as az

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/pymc/__init__.py:48
     43     pytensor.config.gcc__cxxflags = augmented
     46 __set_compiler_flags()
---> 48 from pymc import _version, gp, ode, sampling
     49 from pymc.backends import *
     50 from pymc.blocking import *

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/pymc/gp/__init__.py:15
      1 #   Copyright 2024 The PyMC Developers
      2 #
      3 #   Licensed under the Apache License, Version 2.0 (the "License");
   (...)
     12 #   See the License for the specific language governing permissions and
     13 #   limitations under the License.
---> 15 from pymc.gp import cov, mean, util
     16 from pymc.gp.gp import (
     17     TP,
     18     Latent,
   (...)
     23     MarginalSparse,
     24 )
     25 from pymc.gp.hsgp_approx import HSGP, HSGPPeriodic

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/pymc/gp/cov.py:52
     29 from pytensor.tensor.variable import TensorConstant, TensorVariable
     31 __all__ = [
     32     "Constant",
     33     "WhiteNoise",
   (...)
     49     "Kron",
     50 ]
---> 52 from pymc.pytensorf import constant_fold
     54 TensorLike = Union[np.ndarray, TensorVariable]
     55 IntSequence = Union[np.ndarray, Sequence[int]]

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/pymc/pytensorf.py:59
     56 from pytensor.tensor.variable import TensorConstant, TensorVariable
     58 from pymc.exceptions import NotConstantValueError
---> 59 from pymc.util import makeiter
     60 from pymc.vartypes import continuous_types, isgenerator, typefilter
     62 PotentialShapeType = Union[int, np.ndarray, Sequence[Union[int, Variable]], TensorVariable]

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/pymc/util.py:21
     18 from collections.abc import Sequence
     19 from typing import Any, NewType, Optional, Union, cast
---> 21 import arviz
     22 import cloudpickle
     23 import numpy as np

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/arviz/__init__.py:34
     30 _log = Logger("arviz")
     33 from .data import *
---> 34 from .plots import *
     35 from .plots.backends import *
     36 from .stats import *

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/arviz/plots/__init__.py:2
      1 """Plotting functions."""
----> 2 from .autocorrplot import plot_autocorr
      3 from .bpvplot import plot_bpv
      4 from .bfplot import plot_bf

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/arviz/plots/autocorrplot.py:7
      5 from ..rcparams import rcParams
      6 from ..utils import _var_names
----> 7 from .plot_utils import default_grid, filter_plotters_list, get_plotting_function
     10 def plot_autocorr(
     11     data,
     12     var_names=None,
   (...)
     24     show=None,
     25 ):
     26     r"""Bar plot of the autocorrelation function (ACF) for a sequence of data.
     27 
     28     The ACF plots are helpful as a convergence diagnostic for posteriors from MCMC
   (...)
    117         >>> az.plot_autocorr(data, var_names=['mu', 'tau'], max_lag=200, combined=True)
    118     """

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/arviz/plots/plot_utils.py:15
     11 from scipy.interpolate import CubicSpline
     14 from ..rcparams import rcParams
---> 15 from ..stats.density_utils import kde
     16 from ..stats import hdi
     18 KwargSpec = Dict[str, Any]

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/arviz/stats/__init__.py:3
      1 # pylint: disable=wildcard-import
      2 """Statistical tests and diagnostics for ArviZ."""
----> 3 from .density_utils import *
      4 from .diagnostics import *
      5 from .stats import *

File /opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/arviz/stats/density_utils.py:8
      6 from scipy.fftpack import fft
      7 from scipy.optimize import brentq
----> 8 from scipy.signal import convolve, convolve2d, gaussian  # pylint: disable=no-name-in-module
      9 from scipy.sparse import coo_matrix
     10 from scipy.special import ive  # pylint: disable=no-name-in-module

ImportError: cannot import name 'gaussian' from 'scipy.signal' (/opt/hostedtoolcache/Python/3.9.20/x64/lib/python3.9/site-packages/scipy/signal/__init__.py)

Summary using mean#

# Posterior Summary
summary = az.summary(trace, kind="stats")
summary
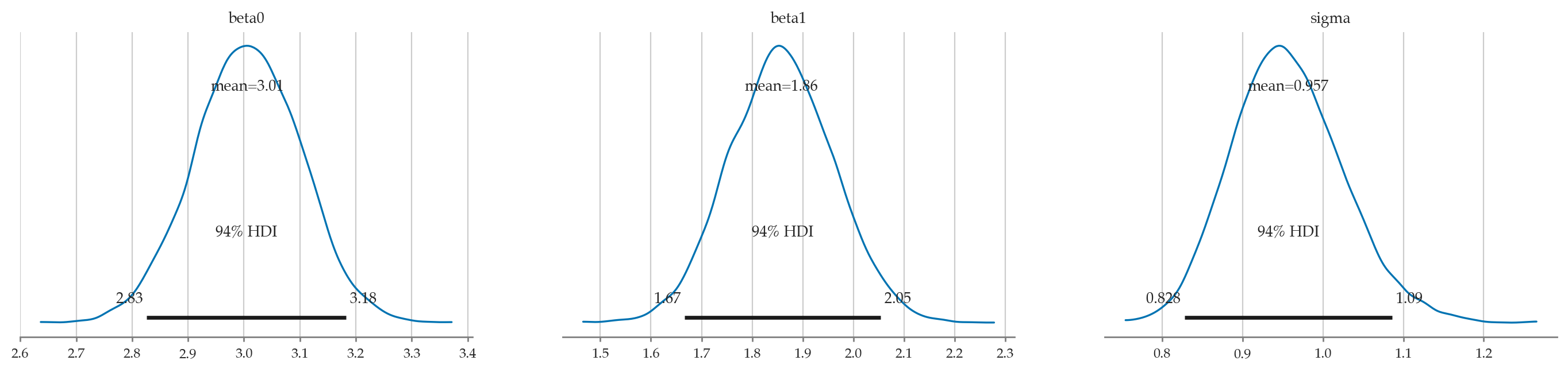
mean sd hdi_3% hdi_97%
beta0 3.006 0.095 2.826 3.183
beta1 1.857 0.104 1.667 2.054
sigma 0.957 0.069 0.828 1.086

Summary using median as focus statistic#

ETI = Equal-Tailed Interval

az.summary(trace, stat_focus="median", kind="stats")
median mad eti_3% eti_97%
beta0 3.006 0.065 2.826 3.183
beta1 1.856 0.070 1.666 2.053
sigma 0.953 0.046 0.837 1.096 
# Plotting posterior
az.plot_posterior(trace, point_estimate="mean", round_to=3);
../_images/c03c6b4083861dbec4f1ff20ab0ddde2eba74a5cd0bc3a6c332d9c3af92fe04c.png
Contents